如图所示，有一电子束从点a处以一定的水平速度飞向竖直放置的荧光屏，将垂直击中荧光屏上的点b，已知电子的质量为m，电量为q.
（1）若在电子束运行途中加一半径为R的圆形磁场，磁感应强度为B，方向垂直于纸面向里，圆心O在点a、b连线上，点O距荧光屏距离为L，为使电子束仍击中荧光屏上的点b，可加一个场强为E的匀强电场，指出此匀强电场的方向和范围，并求出电子束的速度．
（2）现撤去电场，电子束以原速度沿原来方向从a点发射，运动方向在磁场中偏转后击中荧光屏上的点c．求b、c间的距离.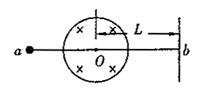
如图3-2-19所示，边长为a的单匝的正方形线圈的磁感应强度为B的匀强磁场中，以OO′边为轴匀速转动，角速度为ω，转轴与磁场方向垂直，线圈电阻为R.求：
图3-2-19
（1）线圈从图示位置转过
的过程中产生的热量Q；
（2）线圈从图示位置转过的过程中通过线圈某截面的电量q.
如图3-11所示，单匝线圈在匀强磁场中绕OO′轴从图示的位置开始匀速转动，已知从图示位置转过π/6时，线圈中的电动势大小为6 V，求：
图3-11
（1）交变电动势的最大值、有效值；
（2）设线圈的电阻为R="1" Ω，角速度ω="100" rad/s，线圈由图示位置转过π/2的过程中通过导线截面的电荷量.
将交变电压u=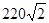
sin100πt V加在灯泡两端，灯泡的额定值为“220 V100 W”，如果不考虑灯丝电阻的变化，求：
（1）通过灯丝电流的最大值；
（2）灯泡的实际功率；
（3）每秒钟电流方向变化的次数；
（4）通过灯丝的电流瞬时值方程.
发电机的转子是匝数为100匝，边长为20 cm的正方形线圈，将它置于磁感应强度B="0.05" T的匀强磁场中，绕着垂直于磁感线方向的轴以ω="100π" rad/s的角速度转动，当线圈平面跟磁场方向垂直时开始计时，线圈和外电路的总电阻R="10" Ω.
(1)写出交流电流瞬时值的表达式；
(2)线圈从计时开始，转过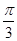
的过程中通过线圈某一截面的电荷量为多少？
一个矩形线圈在匀强磁场中绕垂直于磁场方向的轴匀速转动时，线圈内便产生按正弦规律变化的电流，这就是交流发电机原理.如图3-2-20所示.请思考下列问题：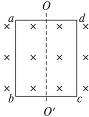
图3-2-20
（1）实际的发电机，为了运转平稳，轴OO′通常位于ad、bc边的中点连线上.若将轴OO′向左或向右平移任意距离（小于或等于ad/2），线圈中是否仍产生规律相同的正弦式电流，为什么？
（2）若将线圈abcd换成等面积的圆形线圈，使其绕位于直径的轴匀速转动，线圈中是否仍产生规律相同的正弦式电流，为什么？
（3）线圈中感应电动势E与时间t的关系表达式的形式是正弦型还是余弦型和什么条件有关？