质量为m的飞机以水平速度v0飞离跑道后逐渐上升，若飞机在此过程中水平速度保持不变，同时受到重力和竖直向上的恒定升力（该升力由其它力的合力提供，不含升力）。今测得当飞机在水平方向的位移为l时，它的上升高度为h。求：
⑴飞机受到的升力大小；
⑵从起飞到上升至h高度的过程中升力所做的功及在高度h处飞机的动能。
(1)水平飞出时速度大小；
（2）落到底端时的速度大小；
（3）从飞出到离开斜面最远处所用的时间．
月球自转一周的时间与月球绕地球运行一周的时间相等，都为T0。我国的“
嫦娥1号”探月卫星于2007年11月7日成功进入绕月运行的“极月圆轨道”，这一圆形轨道通过月球两极上空，距月面的高度为h。若月球质量为M，月球半径为R，万有引力恒量为G。
（1）求“嫦娥1号”绕月运行的周期。
（2）在月球自转一周的过程中，“嫦娥1号”将绕月运行多少圈？
（3）“嫦娥1号”携带了一台CCD摄相机（摄相机拍摄不受光照影响），随着卫星的飞行，摄像机将对月球表面进行连续拍摄。要求在月球自转一周的时间内，将月面各处全部拍摄下来，摄像机拍摄时拍摄到的月球表面宽度至少是多少？
如图所示，轨道ABC被竖直地固定在水平桌面上，A距离水平地面高H =" 0.75" m，C距离水平地面高h =" 0.45" m。一质量m = 0.10kg的小物块自A点从静止开始下滑，从C点以水平速度飞出后落在水平地面上的D点
。现测得C、D两点的水平距离为l =" 0.60" m。不计空气阻力，取g =" 10" m/s2。求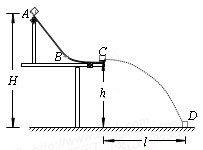
（1）小物块从C点运动到D点经历的时间；
（2）小物块从C点飞出时速度的大小；
（3）小物块从A点运动到C点的过程中克服摩擦力做的功。
如图所示，在倾角为θ = 30o 的光滑斜面的底端有一个固定挡板D，小物体C靠在挡板D上，小物体B与C用轻质弹簧拴接。当弹簧处于自然长度时，B在O点；当B静止时，B在M点，OM = l。在P点还有一小物体A，使A从静止开始下滑，A、B相碰后一起压缩弹簧。A第一次脱离B后最高能上升到N点，ON =" 1.5" l。B运动还会拉伸弹簧，使C物体刚好能脱离挡板D。A、B、
C的质量都是m，重力加速度为g。求
（1）弹簧的劲度系数；
（2）弹簧第一次恢复到原长时B速度的大小；
（3）M、P之间的距离。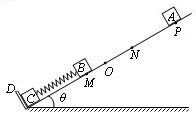
1897年汤姆生通过对阴极射线的研究，发现了电子，从而使人们认识到原子是可分的。汤姆生当年用来测定电子比荷（电荷量e与质量m之比）的实验装置如图所示，真空玻璃管内
C、D为平行板电容器的两极，圆形阴影区域内可由管外电磁铁产生一垂直纸面的匀强磁场，圆形区域的圆心位于C、D中心线的中点，直径与C、D的长度相等。已知极板C、D的长度为L1，C、D间的距离为d，极板右端到荧光屏的距离为L2。由K发出的电子，经A与K之间的高电压加速后，形成一束很细的电子流，电子流沿C、D中心线进入板间区域。
若C、D间无电压，则电子将打在荧光屏上的O点；若在C、D间加上电压U，则电子将打在荧光屏上的P点，P点到O点的距离为h；若再在圆形区域内加一方向垂直于纸面向外、磁感应强度为B的匀强磁场，则电子又打在荧光屏上的O点。不计重力影响。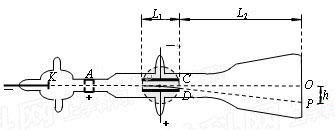
（1）求电子打在荧光屏O点时速度的大小。
（2）推导出电子比荷的表达式。
（3）利用这个装置，还可以采取什么方法测量电子的比荷？