①教育局督学组到学校检查工作，需在高三年级的学号为001·800的学生中抽调
人参加关于学校管理的综合座谈；②该校高三年级这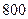
名
学生期中考试的数学成绩有160
在120分以上（包括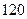
分），480人在120以下90分以上（包括90分），其余的在
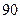分
以下，现欲从中抽出人研讨进一步改进数学教和学的座谈；③该校高三年级这800名学
生参加2010年元旦聚会，要产生20名“幸运之星”．以上三件事，合适的抽样方法依次（ ）
| A．系统抽样，分层抽样，系统抽样 |
| B．系统抽样，系统抽样，简单随机抽样 |
| C．分层抽样，简单随机抽样，简单随机抽样 |
| D．系统抽样，分层抽样，简单随机抽样 |
若椭圆
+
=1(m>n>0)和双曲线
－
=1(a>b>0)有相同的焦点F1、F2，P是两条曲线的一个交点，则|PF1|·|PF2|的值是
| A．m－a | B． (m－a) |
| C．m2－a2 | D． － |
方程
=|x+y－2|表示的曲线是
| A．椭圆 | B．双曲线 |
| C．抛物线 | D．不能确定 |
以椭圆
+
=1的焦点为焦点，离心率e=2的双曲线方程是
A． － ="1" |
B．－ =1 |
C． －="1" |
D．－=1 |
双曲线
－
=1的两焦点为F1、F2，点P在双曲线上，且直线PF1、PF2倾斜角之差为
,则△PF1F2的面积为
A．16 |
B．32 |
| C．32 | D．42 |
若双曲线
－
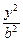=1的实轴长、虚轴长、焦距成等差数列，则双曲线的离心率是
| A．2 | B．3 |
C． |
D． |