如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m <M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
(1)A、B最后的速度大小和方向.
(2)从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小.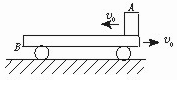
(1)如果磁感应强度B0为已知量,试推出满足条件时t1的表达式(用题中所给物理量的符号表示)
(2)若小球能始终在电场所在空间做周期性运动.则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小.
(3)当小球运动的周期最大时,在图中画出小球运动一个周期的轨迹.
(1)施力F后要想把木板从物体m的下方抽出来,求力F的大小应满足的条件。
(2)如果所施力F=10N,为了把木板从m的下方抽出来,此力的作用时间不得少于多少?
(1)电子离开极板时的动能为多少eV。
(2)极板的长度L。
(1)M从释放开始到第一次着地所用时间
(2)M第3次着地时系统损失的机械能与绳第3次绷直时系统损失的机械能之比
(3)M所走的全部路程(取三位有效数字)
(1)油滴的电性;
(2)油滴在P点得到的初速度大小;
(3) 油滴在第一象限运动的时间和离开第一象限处的坐标值.