在游乐场中,有一大型游戏机叫“跳楼机”,参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40米高处,然后自由释放。为研究方便,可以认为座椅沿轨道自由下落1.2s后,开始受到压缩空气提供的恒定阻力而立即做匀减速运动,且下落到离地面4.0米高处时速度恰好减小到零,然后再让座椅缓慢下落,将游客送回地面,取 ,求:
,求:
(1)座椅自由下落的高度是多少?座椅自由下落结束时刻的速度是多少?
(2)在匀减速阶段,座椅对游客的作用力大小是游客体重的多少倍?
如图16-3-7所示,质量为m的子弹,以速度v水平射入用轻绳悬挂在空中的木块,木块的质量为M,绳长为L,子弹停留在木块中,求子弹射入木块后的瞬间绳子中的张力的大小.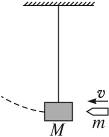
图16-3-7
如图16-2-5所示,如果悬挂球的绳子能承受的最大拉力T0="10" N,球质量m="0.5" kg,L="0.3" m,锤头质量M="0.866" kg,如果锤沿水平方向打击球m,锤头速度多大时才能把绳子打断(设m原来静止,打击后锤头静止,取g="10" m/s2)?
图16-2-5
如图所示的光滑水平面上,质量为M的平板车上依次放有5个质量均为m的小滑块(不计其大小),质量关系为M=5 m,已知平板车长L=1 m,小滑块与平板车间的动摩擦因数μ=9/20,g=10 m/s2。现突然给最左端的小滑块沿平板向右的速度v0,当其相对地的速率降至v0/2时恰好与前方的第2个滑块相碰。碰撞时间极短,碰撞后两滑块的速度变为对方碰撞前的速度(也叫速度交换)。以后将陆续发生小滑块相碰,碰撞时间都很短,碰后均交换速度。最后第5个滑块恰好滑至平板车右端而与平板车相对静止。
(1)求v0的值;
(2)写出第一个小滑块运动中其相对地的最上速度的表达式;
(3)求平板车匀加速运动过程中的位移s。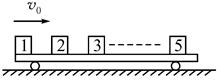
如图所示,质量为m的小物体(可视为质点)放在小车上,它们一起在两堵竖直墙壁之间运动,小车质量为M,且M>m。设车与物体间的动摩擦因数为μ,车与水平面间无摩擦,车与墙壁碰撞后速度反向而且大小不变,且碰撞时间极短。开始时车紧靠在左面墙壁上,物体位于车的最左端,车与物体以共同速度v0向右运动。若两墙壁之间的距离足够长,求:
(1)小车与墙壁第2次碰撞前(物体未从车上掉下)的速度;
(2)要使物体不从车上滑落,车长l应满足的条件。
如图16-3-11所示,质量均为m的A、B两个弹性小球,用长为2l不可伸长的轻绳连接,现把AB两球置于距地面高H处(H足够大)间距为l,当A球自由下落的同时,B球以速度v0指向A球水平抛出,求:
图16-3-11
(1)两球从开始运动到相碰,A球下落的高度;
(2)A、B两球碰撞(碰撞时无机械能损失)后,各自速度的水平分量;
(3)轻绳拉直过程中,B球受到绳子拉力冲量的大小.