用数学归纳法证明: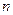 为正偶数时,
为正偶数时,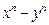 能被
能被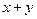 整除.
整除.
在极坐标系中,圆C的方程为ρ=2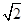 sin
sin ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的方程为y=2x+1,判断直线l和圆C的位置关系.
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的方程为y=2x+1,判断直线l和圆C的位置关系.
在极坐标系中,设圆ρ=3上的点到直线ρ(cosθ+ sinθ)=2的距离为d.求d的最大值.
sinθ)=2的距离为d.求d的最大值.
求以点A(2,0)为圆心,且过点B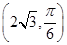 的圆的极坐标方程.
的圆的极坐标方程.
如图,AB是半径为1的圆的一条直径,C是此圆上任意一点,作射线AC,在AC上存在点P,使得AP·AC=1,以A为极点,射线AB为极轴建立极坐标系.
(1)求以AB为直径的圆的极坐标方程;
(2)求动点P的轨迹的极坐标方程;
(3)求点P的轨迹在圆内部分的长度.
求极坐标方程分别为ρ=cosθ与ρ=sinθ的两个圆的圆心距.