跳伞运动员从350m的高空离开飞机,自由下落一段距离后才打开伞。设开伞后以2m/s2的加速度匀减速下降,到达地面时速度为4m/s,求他下落的总时间及自由下落的距离。(g取10m/s2)
图12-2-9(a)表示一列简谐波在介质中传播时,某一质点a的振动图象,请你在(b)图中作出这列简谐波在t=0时刻的波形图(质点a画在坐标原点上).
图12-2-9
一列横波在某时刻的波形图如图12-2-7所示.若此时刻质点a的振动方向向下,则波向什么方向传播?
图12-2-7
在波的传播方向上有两个质点P和Q,它们的平衡位置相距s="1.2" m,且大于一个波长,介质中的波速为v="2" m/s,P和Q的振动图线如图12-3-6所示,求振动周期的最大值,并画出t=0时的波的图象.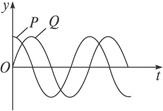
图12-3-6
在图12-3-5所示的图象中,实线是一列简谐横波在某一时刻的图象,经过t="0.2" s后这列波的图象如图中虚线所示,求这列波的波速.
图12-3-5
某人想听到自己发出的声音的回声,若已知声音在空气中的传播速度为340 m/s,那么他至少要离障碍物多远?(原声与回声区分的最短时间0.1 s)