太阳与月球的直径分别为1.39×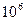 km和3.5×
km和3.5×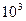 km.设日全食时太阳到地面的距离为1.5×
km.设日全食时太阳到地面的距离为1.5×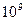 km,月球到地面的距离为3.8×
km,月球到地面的距离为3.8×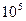 km,试计算地面上能见到日全食区域的面积(可把该区域的地面视为平面).
km,试计算地面上能见到日全食区域的面积(可把该区域的地面视为平面).

某同学星期日沿平直的公路从学校所在地骑自行车先后到甲、乙两位同学家去拜访他们,位移时间图象如图1所示。试描述他的运动过程,在图2中画出他的速度时间图象。
光在空气中的速度可以认为等于光在真空中的速度,声音在空气中的传播速度是340m/s,一个人看到闪电后5s听到雷声,打雷的地方离他大约多远?
右表是客运轮船在九江至武汉之间往返航行的航班运行时刻表,最右边一列是自九江起的公里数。根据表中数据,估算武汉至九江间长江的平均流速为多大?
一辆汽车以20m/s的速度沿平直的公路从甲地开往乙地,又以30m/s的速度从乙地开往丙地。已知甲、乙两地间的距离与乙、丙两地间的距离相等。求该汽车在从甲地开往丙地的过程中平均速度的大小。
有一位同学是这样解的: m/s=25m/s。请问上述解法正确吗?为什么?应该如何解?
m/s=25m/s。请问上述解法正确吗?为什么?应该如何解?