移动公司进行促销活动,促销方案是:顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为20%,中奖后移动公司返还顾客现金1000元。小李购买一部价格为2400元的手机,只能获得两张奖券,于是小李补偿50元给同事购买600元的小灵通,可以获得3张奖券,记小李抽奖后的实际开支为 元。
元。
(1)求 的分布列;
的分布列;
(2)试说明小李出资50元便增加一张奖券是否划算?
是否存在一个等比数列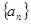 同时满足下列三个条件:
同时满足下列三个条件:
①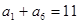 且
且 ;
;
②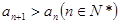 ;
;
③至少存在一个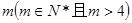 ,使得
,使得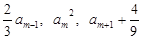 依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
(本小题满分12分)
某工厂生产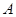 、
、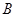 两种产品,计划每种产品的生产量不少于15千克,已知生产
两种产品,计划每种产品的生产量不少于15千克,已知生产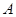 产品1千克要用煤9吨,电力4千瓦,3个工作日;生产
产品1千克要用煤9吨,电力4千瓦,3个工作日;生产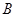 产品1千克要用煤4吨,电力5千瓦,10个工作日。又知生产出
产品1千克要用煤4吨,电力5千瓦,10个工作日。又知生产出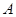 产品1千克可获利7万元,生产出
产品1千克可获利7万元,生产出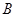 产品1千克可获利12万元,现在工厂只有煤360吨,电力200千瓦,300个工作日,
产品1千克可获利12万元,现在工厂只有煤360吨,电力200千瓦,300个工作日,
(1)列出满足题意的不等式组,并画图;
(2)在这种情况下,生产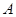 、B产品各多少千克能获得最大经济效益.
、B产品各多少千克能获得最大经济效益.
在△ABC中,内角 所对的边分别为
所对的边分别为 ,已知
,已知 .
.
(1)求证: 成等比数列;
成等比数列;
(2)若 ,求△
,求△ 的面积S.
的面积S.
已知函数 ,
, ,且
,且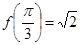
求 的值;
的值;
设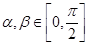 ,
, ,
,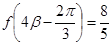 ,求
,求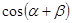 的值.
的值.
某寄宿制学校的一间宿舍里住着若干名学生,其中一人担任舍长.元旦时,该宿舍里的每名学生互赠一张贺卡,且每人又赠给宿舍楼的每位管理员一张贺卡,每位管理员也回赠舍长一张贺卡,这样共用去了51张贺卡,问这间宿舍里住有多少名学生?