如图5-13所示,斜劈B的倾角为30°,劈尖顶着竖直墙壁静止于水平地面上,现将一个质量与斜劈质量相同、半径为r的球A放在墙面与斜劈之间,并从图示位置由静止释放,不计一切摩擦,求此后运动中
(1)斜劈的最大速度.
(2)球触地后弹起的最大高度。(球与地面作用中机械能的损失忽略不计)
(8分) 已知地球的半径为R,自转角速度为 ,地球表面的重力加速度为g,在赤道上空一颗相对地球静止的同步卫星离地面的高度h是多少?(用以上三个量表示)
,地球表面的重力加速度为g,在赤道上空一颗相对地球静止的同步卫星离地面的高度h是多少?(用以上三个量表示)

如图,质量为M=1kg的平板车左端放有一质量为m=2kg的铁块,铁块与车之间的动摩擦因数u=0.5。开始时车和铁块以速度 =6m/s在光滑水平面上向右运动,并使车与墙发生正碰,设碰撞时间极短,且碰后车的速率不变,车身足够长致使铁块始终不能与墙相碰。求
=6m/s在光滑水平面上向右运动,并使车与墙发生正碰,设碰撞时间极短,且碰后车的速率不变,车身足够长致使铁块始终不能与墙相碰。求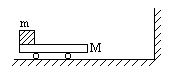
(1)铁块相对于车的总路程。
(2)小车和墙第一次相碰后所走的总路程。
一颗质量为m的子弹,沿水平方向射入一块质量为9m的木块,木块在子弹速度方向上的长度为d,试求:
(1)若木块牢牢固定,子弹以速度v水平射入,钻入d/2停下,则木块对子弹的阻力多大?(设子弹在木块中相对木块运动时所受阻力恒定)
(2)欲使子弹穿过木块,子弹刚水平射入木块的速度v1至少要多大?
(3)若木块固定,子弹以速度2v水平射入,则子弹穿过木块后的速度多大?
(4)在第(3)问的情况下,子弹穿过木块所用的时间是多长?
(5)若木块可在水平面上无摩擦地自由滑动,子弹水平射入的速度为v,则要经多长时间子弹将留在木块里跟木块相对静止?
(6)在第(5)问的情况下,子弹进入木块的深度是d的几分之几?

如图所示,光滑水平面上有A、B两辆小车,质量mc=0.50kg的小球用0.50m长的细线悬挂在A车的支架上.已知 =1.0kg,开始时,B车静止,A车以
=1.0kg,开始时,B车静止,A车以 =4m/s的速度驶向B车并与其正碰后粘在一起.若碰撞时间极短.且不计空气阻力,取g=10m/
=4m/s的速度驶向B车并与其正碰后粘在一起.若碰撞时间极短.且不计空气阻力,取g=10m/ .求小球C摆起的最大高度.
.求小球C摆起的最大高度.