(1)求右焦点坐标是(2,0),且经过点(－2,－
)的椭圆C的标准 方程；
(2)对(1)中的椭圆C,设斜率为1的直线l交椭圆C于A、B两点,AB的中点为M,证明:当直线l平行移动时,动点M在一条过原点的定直线上；
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
（本小题满分12分）现有正整数1，2，3，4，5，…n，一质点从第一个数1出发顺次跳动，质点的跳动步数通过抛掷骰子来决定：骰子的点数小于等于4时，质点向前跳一步；骰子的
点数大于
4时，质点向前跳两步.
（I）若抛掷骰子二次，
质点到达的正整数记为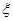
，求E；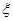
（II）求质点恰好到达正整数5的概率.
（本小题满分12分）如图三棱柱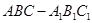
中，底面
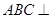侧面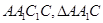
为等边三角形，
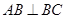且AB=BC，三棱锥
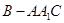的体积为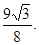
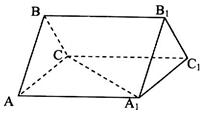
（I）求证：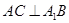
；
（II）求直线
与平面BAA1所成角的正弦值.
（本小题满分12分）设
是单调递增的等差数列，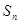
为其前n项和，且满足
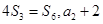是
的等比中项.
（I）求数列的通项公式；
（II）是否存在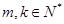
，使
？说明理由；
（III）若数列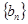
满足
求数列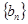的通项公式.
（本小题满分12分）
已知向量
且满足
（I）求函数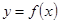
的单调递增区间；
（II）设
的内角A满足
且
，求边BC的最小值.
（本小题满分10分）
已知整数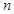
≥4,集合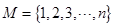
的所有3个元素的子集记为
.
(1)当
时,求集合
中所有元素之和.
(2)设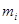
为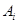
中的最小元素,设
=
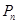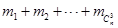,试求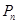.