如图15所示,水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104 N/C。现有一电荷量q=+1.0×10-4C,质量m=0.10 kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体运动到圆形轨道最低点B时的速度vB=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50,重力加速度g=10m/s2。求:
(1)带电体运动到圆形轨道的最低点B时,圆形轨道对带电体支持力的大小;
(2)带电体在水平轨道上的释放点P到B点的距离;
(3)带电体第一次经过C点后,落在水平轨道上的位置到B点的距离。
如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽。薄铁板的长为2.8m、质量为10kg。已知滚轮与铁板与铁板工作台面间的动摩擦因数分别为0.3和0.1。铁板从一端放入工作台的砂轮下,工作时砂轮对铁板产生恒定的竖直向下的压力为100N,在砂轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽。已知滚轮转动的角速度恒为5rad/s。
(1)通过分析计算,说明铁板将如何运动,
(2)加工一快铁板需要多少时间,
(3)加工一快铁板电动机要消耗多少电能。(不考虑电动机自身的能耗)
|
如图所示,在同一竖直平面内两正对着的相同半圆光滑轨道,相隔一定的距离,虚线沿竖直方向,一小球能在其间运动,今在最高点与最低点各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来,当轨道距离变化时,测得两点压力差与距离x的图像如图,g以10m/s2,不计空气阻力,求:
(1)小球的质量为多少?
(2)若小球在最低点B的速度为20m/s,为使 小球能沿轨道运动,x的最大值为多少?
一简谐横波在时刻t=0时的波形图象所示,传播方向自左向右,已知t2=0.6s末,A点出现第三次波峰。试求:
(1)该简谐波的周期;
(2)该简谐波传播到B点所需的时间;
(3)B点第一次出现波峰时,A点经过的路程。
如图所示,粗细均匀竖直放置的U形玻璃管左上端封闭,右上端开口。当温度为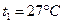 时,管内用水银封闭着长L1=8cm的空气柱,这时两管内水银面等高,已知大气压强为
时,管内用水银封闭着长L1=8cm的空气柱,这时两管内水银面等高,已知大气压强为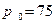 cmHg。
cmHg。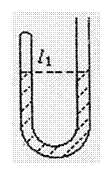
(1)温度T2多高时,被封闭的气柱长变为L2=8.5cm?
(2)保持温度t2不变,从开口端再注入多高的水银柱,气柱长可变回8cm?
如图9所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面倾角为α,已知星球半径为R,万有引力常量为G,求: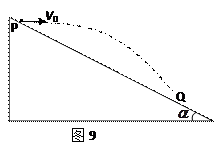
(1)该星球表面的重力加速度g
(2)该星球的密度ρ
(3)该星球的第一宇宙速度v