已知函数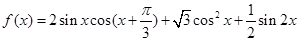 .
.
(1)求函数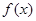 的最小正周期;
的最小正周期;
(2)求函数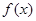 的单调递增区间.
的单调递增区间.
在某高校自主招生考试中,所有选报II类志愿的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为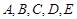 五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为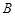 的考生有
的考生有 人.
人.
(1)求该考场考生中“阅读与表达”科目中成绩为 的人数;
的人数;
(2)若等级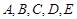 分别对应
分别对应 分,
分,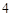 分,
分,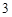 分,
分,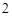 分,
分,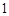 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知在本考场参加测试的考生中,恰有两人的两科成绩均为 .在至少一科成绩为
.在至少一科成绩为 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为 的概率.
的概率.
已知一个动点M在圆 上移动,它与定点Q(4,0)所连线段的中点为P.
上移动,它与定点Q(4,0)所连线段的中点为P.
(1)求点P的轨迹方程.
(2)过定点(0,-3)的直线l与点P的轨迹交于不同的两点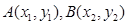 且满足
且满足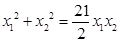 ,求直线l的方程.
,求直线l的方程.
在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC, 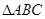 是等边三角形.
是等边三角形.
(1)在棱AC上是否存在一点M,使直线AB1//平面BMC1,请证明你的结论.
(2)设D为AC的中点,P为AB1上的动点, 且AB=2,AA1=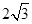 .求三棱锥P-BC1D的体积.
.求三棱锥P-BC1D的体积.
如图1矩形APCD中,AD=2AP,B为PC的中点,将三角形APB折沿AB折起,使得PD=PC,如图2.
(1)若E为PD中点,证明CE//平面APB;
(2)证明:平面APB 平面ABCD.
平面ABCD.