某人上午7:00乘汽车以匀速v1千米/时(30≤v1≤100)从A地出发到距A地300千米的B地,在B地不作停留,然后骑摩托车以匀速v2千米/时 (4≤v2≤20)从B地出发到距B地50千米的C地,计划在当天16:00至21:00时到达C地.设乘汽车、摩托车行驶的时间分别是x、y小时,则在xOy坐标系中,满足上述条件的x、y的范围用阴影部分表示正确的是( )
对任意的实数 ,记
,记 若
若 ,其中奇函数
,其中奇函数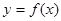 在
在 时有极小值
时有极小值 ,
,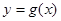 是正比例函数,函数
是正比例函数,函数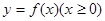 与函数
与函数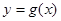 的图象如图所示,则下列关于函数
的图象如图所示,则下列关于函数 的说法中,正确的是( )
的说法中,正确的是( )
A. 为奇函数 为奇函数 |
B. 有极大值 有极大值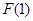 且有极小值 且有极小值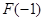 |
C. 的最小值为 的最小值为 且最大值为 且最大值为 |
D. 在 在 上不是单调函数 上不是单调函数 |
已知函数f(x)=Acos(ωx+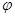 )(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,|
)(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,|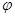 |<
|<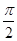 ,为了得到函数f(x)的图像,只要将函数g(x)=2(
,为了得到函数f(x)的图像,只要将函数g(x)=2(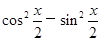 )(x∈R)的图像上所有的点()
)(x∈R)的图像上所有的点()
A.向右平移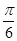 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的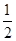 倍,纵坐标不变 倍,纵坐标不变 |
B.向右平移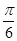 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移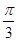 个单位长度,再把得所各点的横坐标缩短到原来的 个单位长度,再把得所各点的横坐标缩短到原来的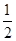 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移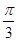 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
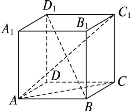
在正方体ABCD-A1B1C1D1中,给出以下结论:
①AC∥平面A1C1B ②AC1与BD1是异面直线
③AC⊥平面BB1D1D ④平面ACB1⊥平面BB1D1D
其中正确结论的个数是()
| A.1 | B.2 | C.3 | D.4 |
已知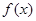 在
在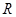 上是奇函数,且满足
上是奇函数,且满足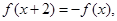 当
当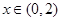 时,
时,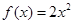 ,则
,则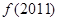 等于 ( )
等于 ( )
A.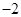 |
B.2 | C.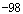 |
D.98 |
数列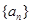 是公差不为0的等差数列,且
是公差不为0的等差数列,且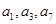 为等比数列
为等比数列 的连续三项,则数列
的连续三项,则数列 的公比为()
的公比为()
A. |
B.4 | C.2 | D.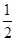 |