小明到他父亲的木工房,看到一个棱长为50 cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少? 
对于在区间 上有意义的两个函数
上有意义的两个函数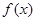 和
和 ,如果对于任意的
,如果对于任意的 ,都有
,都有 ,则称
,则称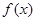 与
与 在区间
在区间 上是接近的两个函数,否则称它们在
上是接近的两个函数,否则称它们在 上是非接近的两个函数。现有两个函数
上是非接近的两个函数。现有两个函数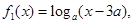 ,
,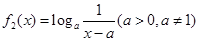 ,且
,且 与
与 在
在 都有意义.
都有意义.
(1)求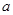 的取值范围;
的取值范围;
(2)讨论 与
与 在区间
在区间 上是否是接近的两个函数.
上是否是接近的两个函数.
下图是一个二次函数 的图象.写出
的图象.写出 的解集;
的解集;
(2)求这个二次函数的解析式;
(3)当实数 在何范围内变化时,
在何范围内变化时,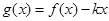 在区间
在区间  上是单调函数.
上是单调函数.
已知二次函数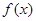 的最小值为1,且
的最小值为1,且 .
.
(1)求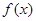 的解析式;
的解析式;
(2)若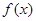 在区间
在区间 上不单调,求实数
上不单调,求实数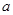 的取值范围;
的取值范围;
(3)在区间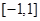 上,
上,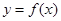 的图像恒在
的图像恒在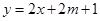 的图像上方,试确定实数
的图像上方,试确定实数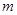 的取值范围.
的取值范围.
已知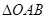 中,点
中,点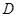 在线段
在线段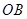 上,且
上,且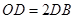 ,延长
,延长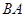 到
到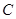 ,使
,使 .设
.设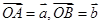 .
.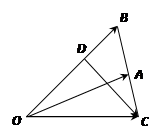
(1)用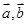 表示向量
表示向量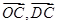 ;
;
(2)若向量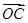 与
与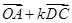 共线,求
共线,求 的值.
的值.
某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价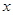 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数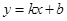 的关系(图象如下图所示).
的关系(图象如下图所示).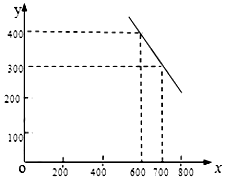
(1)根据图象,求一次函数 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,
①求S关于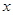 的函数表达式;
的函数表达式;
②求该公司可获得的最大毛利润,并求出此时相应的销售单价.