(1)所加交流电频率应是多大?
(2)离子离开加速器时动能多大?
(3)若两D型盒间距为d,两者间电场为匀强电场,假设粒子在电场中加速的时间不忽略,但又不影响高频电源与粒子偏转间的同步关系,求某个粒子从加速开始到从D形盒中出来,所需的总时间?
如图6-8-28所示,直杆上O1O2两点间距为L,细线O1A长为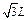 ,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度ω转动?
,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度ω转动?
如图所示为某一电路的俯视图,空中存在着竖直向下的匀强磁场,磁感应强度为B,在同一水平面上固定着平行金属轨道MN和PQ,两道轨间的距离为l。金属杆ab沿垂直轨道方向放置在两轨道上,金属杆ab在MN和PQ间的电阻为r,且与轨道接触良好。与两轨道连接的电路中有两个阻值相同的电阻R1和R2,且R1=R2=R,电阻R2与一电容器串联,电容器的电容为C,轨道光滑且不计轨道的电阻。若金属杆ab在某一水平拉力的作用下以速度v沿金属轨道向右做匀速直线运动,那么在此过程中:
(1)流过电阻R1的电流为多大?
(2)电容器的带电量为多大?
(3)这个水平拉力及其功率分别为多大?
如图甲所示,空间存在竖直向上的磁感应强度为B的匀强磁场,ab、cd是相互平行的间距为l的长直导轨,它们处于同一水平面内,左端由金属丝bc相连,MN是跨接在导轨上质量为m的导体棒,已知MN与bc的总电阻为R,ab、cd的电阻不计。用水平向右的拉力使导体棒沿导轨做匀速运动,并始终保持棒与导轨垂直且接触良好。图乙是棒所受拉力和安培力与时间关系的图象,已知重力加速度为g。

(1)求导体棒与导轨间的动摩擦因数μ;
(2)已知导体棒发生位移s的过程中bc边上产生的焦耳热为Q,求导体棒的电阻值;
(3)在导体棒发生位移s后轨道变为光滑轨道,此后水平拉力的大小仍保持不变,图丙中Ⅰ、Ⅱ是两位同学画出的导体棒所受安培力随时间变化的图线。判断他们画的是否正确,若正确请说明理由;若都不正确,请你在图中定性画出你认为正确的图线,并说明理由。(要求:说理过程写出必要的数学表达式)
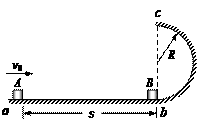 如图所示,半径R = 0.1m的竖直半圆形光滑轨道bc与水平面ab相切。
如图所示,半径R = 0.1m的竖直半圆形光滑轨道bc与水平面ab相切。
质量m = 0.1㎏的小滑块B放在半圆形轨道末端的b点,另一质量也为m= 0.1kg的小滑块A,以v0 = 2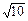 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
(1)A与B碰撞前瞬间的速度大小vA;
(2)碰后瞬间,A、B共同的速度大小v;
(3)在半圆形轨道的最高点c,轨道对A、B
的作用力N的大小。
如图所示,在y>0的区域内有沿y轴正方向的匀强电场,在y<0的区域 内有垂直坐标平面向里的匀强磁场。一电子(质量为m、电量为e)从y轴上A点以沿x轴正方向的初速度v0开始运动。当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点。C、D两点均未在图中标出。已知A、C点到坐标原点的距离分别为d、2d。不计电子的重力。求
内有垂直坐标平面向里的匀强磁场。一电子(质量为m、电量为e)从y轴上A点以沿x轴正方向的初速度v0开始运动。当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点。C、D两点均未在图中标出。已知A、C点到坐标原点的距离分别为d、2d。不计电子的重力。求
(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)电子从A运动到D经历的时间t.