用密度为d、电阻率为ρ、横截面积为A的薄金属条制成边长为L的闭合正方形框
。如图所示，金属方框水平放在磁极的狭缝间，方框平面与磁场方向平行。设匀强磁场仅存在于相对磁极之间，其他地方的磁场忽略不计。可认为方框的
边和
边都处在磁极之间，极间磁感应强度大小为B。方框从静止开始释放，其平面在下落过程中保持水平（不计空气阻力）。
（1）求方框下落的最大速度vm（设磁场区域在数值方向足够长）；
（2）当方框下落的加速度为
时，求方框的发热功率P；
（3）已知方框下落时间为t时，下落高度为h，其速度为vt（vt<vm）。若在同一时间t内，方框内产生的热与一恒定电流I0在该框内产生的热相同，求恒定电流I0的表达式。
如图13-5-8所示，光滑绝缘细杆竖直放置，它与以正点电荷Q为圆心的某一圆周交于B、C两点，质量为m，电荷量为-q的有孔球从杆上的A点无初速下滑，已知q≤Q，
=h.小球滑到B点时速大小为
.求：
图13-5-8
（1）小球由A到B的过程中电场力做的功；
（2）已知Ub=Uc，求A、C两点间的电势差.
如图所示是一种电磁泵的原理图，截面为矩形的导管PQ是运送导电液体用的，它的截面长为A．宽为b．导管的上、下两面有两块导体C．D，处于相对的位置，分别与电源的正、负极相连，通过的电流大小为I．导管的其他部分都是绝缘的．导管的通电部分位于匀强磁场中，磁场的方向与电流方向垂直，水平向右，大小为B，磁场区域的宽度为l．设液体在导管内流动时受到的阻力f的大小跟液体的流动速度v成正比，比例系数为k(即f=kv)．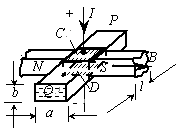
(1)导管内导电液体向哪个方向流动，稳定的流动速度v0多大？
(2)已知导管内液体单位体积内的参与导电的自由电荷的数目为n、每个自由电荷的电荷量为q．求参与导电的自由电荷定向移动的平均速率．
如图所示，半径为R的光滑绝缘圆环固定在竖直平面内，在环的底端B点固定一个带正电的小球，环上还套有一个质量为m，带等量正电荷的小球，现将小球从A点(半径OA水平)由静止释放开始运动，当运动到C点(∠AOC＝
)时获得的最大动能为Ekm，求：
(1)小球从位置A运动到位置C的过程中所受静电力做的功W；
(2)小球在A点刚释放时运动的加速度a；
(3)小球在位置C时受到圆环对它的作用力．
足够大的平行金属板竖直放置，两板相距d，分别与直流电源的正负极相连，电源电动势E，质量为m、电量为－q的质点：沿着右板的边缘从a点开始被竖直上抛，最后在左板与a点等高的b点与左板相碰．试计算：．
(1)带点质点由a到b运动过程中，到达的最高点，相对于ab的高度多大？最高点与右板相距多远？
(2)质点与左板相碰前的瞬时速度的大小和方向．
如图1所示，一对足够长的平行光滑导轨放置在水平面上，两轨道间距l=0.20m，定值电阻阻值R=1.0Ω．有一金属杆静止地放在轨道上，与两轨道垂直且接触良好，金属杆与轨道的电阻皆可忽略不计，整个装置处于磁感应强度为B=0.50T的匀强磁场中，磁场方向垂直轨道面向下．现用一外力F沿轨道方向拉杆，使之做匀加速运动，测得力F与时间t的关系如图2所示．求：
(1)杆的质量m和加速度
(2)在杆从静止开始运动的20s的时间内，通过电阻R的电量．