已知函数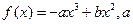 、
、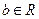 。
。
(1)讨论函数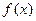 的奇偶性(只写结论,不要求证明);
的奇偶性(只写结论,不要求证明);
(2)在构成函数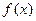 的映射
的映射 中,当输入值为
中,当输入值为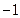 和2时分别对应的输出值为
和2时分别对应的输出值为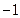 和
和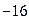 ,求
,求 、
、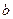 的值;
的值;
(3)在(2)的条件下,求函数 (
(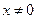 )的最大值。
)的最大值。
设无穷数列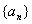 的首项
的首项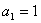 ,前
,前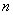 项和为
项和为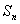 (
(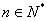 ),且点
),且点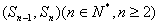 在直线
在直线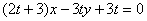 上(
上(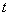 为与
为与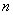 无关的正实数).
无关的正实数).
(1)求证:数列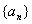 (
(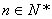 )为等比数列;
)为等比数列;
(2)记数列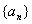 的公比为
的公比为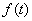 ,数列
,数列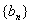 满足
满足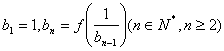 ,设
,设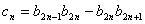 ,求数列
,求数列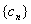 的前
的前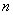 项和
项和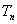 ;
;
(3)若(2)中数列{Cn}的前n项和Tn当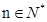 时不等式
时不等式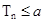 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
已知双曲线x2-y2=2若直线n的斜率为2 ,直线n与双曲线相交于A、B两点,线段AB的中点为P,
(1)求点P的坐标(x,y)满足的方程(不要求写出变量的取值范围);
(2)过双曲线的左焦点F1,作倾斜角为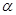 的直线m交双曲线于M、N两点,期中
的直线m交双曲线于M、N两点,期中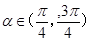 ,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角
,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角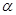 的表达式。
的表达式。
求证:
(1)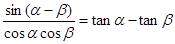
(2)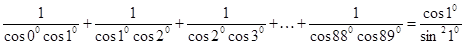
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=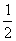 (弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为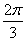 ,弦长等于9米的弧田.
,弦长等于9米的弧田.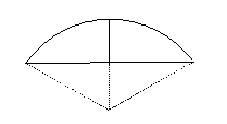
(1)计算弧田的实际面积;
(2)按照《九章算术》中弧田面积的经验公式计算所得结果与(1)中计算的弧田实际面积相差多少平方米?(结果保留两位小数)
已知函数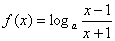 (其中
(其中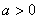 且
且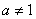 ),
),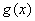 是
是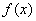 的反函数.
的反函数.
(1)已知关于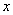 的方程
的方程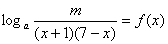 在区间
在区间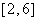 上有实数解,求实数
上有实数解,求实数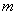 的取值范围;
的取值范围;
(2)当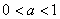 时,讨论函数
时,讨论函数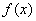 的奇偶性和增减性;
的奇偶性和增减性;
(3)设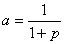 ,其中
,其中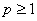 .记
.记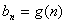 ,数列
,数列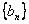 的前
的前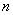 项的和为
项的和为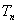 (
(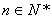 ),
),
求证: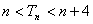 .
.