如图所示,质量为m的小球P位于距水平地面高度H处,在水平地面的上方存在一定厚度的“作用力区域”,如图中的虚线部分。当小球进入“作用力区域”后将受到竖直向上的恒定作用力F,F=5mg,F对小球的作用刚好使从静止释放的小球不与水平地面接触。H=25 m,g=10 m / s2。 求:
(1)作用力区域的厚度h=?
(2)小球从静止释放后的运动是周期性的运动,周期T=?(即从P点开始运动到又回到P点所用的时间)
神舟五号载入飞船在绕地球飞行的第5圈进行变轨,由原来的椭圆轨道变为距地面高度h=342km的圆形轨道。已知地球半径R=6.37×103km,地面处的重力加速度g=10m/s2。试导出飞船在上述圆轨道上运行的周期T的公式(用h、R、g表示),然后计算周期T的数值(保留两位有效数字)。
两块平行金属板MN、PQ水平放置,两板间距为d、板长为l,在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与PQ在同一水平线上,顶点A与MN在同一水平线上,如图所示.一个质量为m、电量为+q的粒子沿两板中心线以初速度v0水平射入,若在两板间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,BD= AB,并垂直AC边射出(不计粒子的重力).求:
AB,并垂直AC边射出(不计粒子的重力).求:
(1)两极板间电压;
(2)三角形区域内磁感应强度;
(3)若两板间不加电压,三角形区域内的磁场方向垂直纸面向外.要使粒子进入磁场区域后能从AB边射出,试求所加磁场的磁感应强度最小值.
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,侧得小球经时间t落到斜坡上另一点Q,斜面的倾角为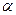 ,已知该星球半径为R,万有引力常量为G,求:
,已知该星球半径为R,万有引力常量为G,求: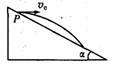
(1)该星球表面的重力加速度g;
(2)该星球的密度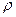 ;
;
(3)该星球的第一宇宙速度v;
(4)人造卫星绕该星球表面做匀速圆周运动的最小周期T.
甲:长为1.6m的细线系一质量为lkg的小球在竖直平面内做圆周运动,求小球通过最高点的速度至少为多大?(g取10m/s2)
下面是甲同学对该题的解法:
解:则小球在最高点时,受到的合力最小值等于重力大小,所以在最高点速度有最小值。此时 ,解得
,解得
小球在最高点速度至少为4m/s
你认为这个解法正确吗?并说明理由。
乙:长为1.6m的细杆栓一质量为1kg的小球在竖直平面内做圆周运动,求小球通过最高点的速度至少为多大?(g取10m/s2)
下面是乙同学对该题的解法:
解:则小球在最高点时,受到的合力最小值等于重力大小,所以在最高点速度有最小值。此时 ,解得
,解得
小球在最高点速度至少为4m/s
你认为这个解法正确吗?并说明理由。
在一个行星上,一昼夜的时间为T0="6" h。若在行星上用弹簧秤测同一物体的重力,发现在赤道上仅为在两极的90%.设想该行星的自转角速度加快到某一值时,赤道上的物体会自动飘起来.试计算这时行星上的一昼夜是多长?