“神舟”六号飞船完成了预定空间科学和技术试验任务后，返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回。在离地l0km的高度返回舱打开阻力降落伞减速下降，返回舱在这一过程中所受空气阻力与速度的平方成正比，比例系数（空气阻力系数）为k。已知返回舱的总质量M =3000kg，所受空气浮力恒定不变，且认为竖直降落。从某时刻起开始计时，返回舱的运动v — t图象如图中的AD曲线所示，图中AB是曲线在A点的切线，切线交于横轴于B点的坐标为（ 10，0 ），CD是AD的渐近线，亦是平行于横轴的直线，交纵轴于C点，C点的坐标为（ 0，6 ）。请解决下列问题：（取g=10 m/ s2）
（1）在初始时刻v0 = 160m/s时，它的加速度多大?
（2）推证空气阻力系数k的表达式并算出其数值；
（3）返回舱在距地高度h = 10m时, 飞船底部的4个反推力小火箭点火工作, 使其速度由6m/s迅速减至1m/s后落在地面上。若忽略燃料质量的减少对返回舱总质量的影响, 并忽略此阶段速度变化而引起空气阻力的变化, 试估算每支小火箭的平均推力（计算结果取两位有效数字）。
（原子量为232.0372）衰变为
（原子量为228.0287）时，释放出α粒子（
的原子量为4.0026），写出核反应方程，并求出衰变过程中释放出多少能量.
一速度为v的高速α粒子（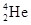
）与同方向运动的氖核（
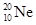）发生弹性正碰，碰后α粒子恰好静止。求碰撞前后氖核的速度（不计相对论修正）。
太阳现正处于主序星演化阶段.它主要是由电子和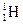
、
等原子核组成.维持太阳辐射的是它内部的核聚变反应，核反应方程是
释放的核能，这些核能最后转化为辐射能.根据目前关于恒星演化的理论，若由于聚变反应而使太阳中的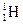核数目从现有数减少10％，太阳将离开主序星阶段而转入红巨星的演化阶段.为了简化，假定目前太阳全部由电子和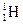核组成.
（1）为了研究太阳演化进程，需知道目前太阳的质量M.已知地球半径R＝6.4×106 m，地球质量m＝6.0×1024 kg，日地中心的距离r＝1.5×1011 m，地球表面处的重力加速度g＝10m/s2，1年约为3.2×107秒，试估算目前太阳的质量M.
（2）已知质子质量mp＝1.6726×10
27 kg，质量mα＝6.6458×1027 kg，电子质量 me＝0.9×1030 kg，光速c＝3×108 m/s.求每发生一次题中所述的核聚变反应所释放的核能.
（3）又知地球上与太阳垂直的每平方米截面上，每秒通过的太阳辐射能w＝1.35×103 W/m2.试估算太阳继续保持在主序星阶段还有多少年的寿命.（估算结果只要求一位有效数字.）
光滑水平面上一平板车质量为M＝50kg，上面站着质量m＝70kg的人，共同以速度v0匀速前进，若人相对车以速度v=2m/s向后跑，问人跑动后车的速度改变了多少?
高压采煤水枪出水口的截面积为S，水的射速为v，射到煤层上后，水速度为零.若水的密度为ρ，求水对煤层的冲力。