如图甲所示，在场强大小为E、方向竖直向下的匀强电场内存在一个半径为R的圆形区域，O点为该圆形区域的圆心，A点是圆形区域的最高点，B点是圆形区域最右侧的点．在A点由放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷，电荷的质量为m，电量为q，不计电荷的重力．
⑴正电荷以多大的速率发射，才能经过图中的P点（图甲中∠POA=θ为已知）？
⑵在问题⑴中，电荷经过P点的动能是多大？
⑶若在圆形区域的边缘有一接收屏CBD，其中C、D分别为接收屏上最边缘的两点(如图乙所示)，且∠COB=∠BOD=30°．则该屏上接收到的正电荷的最大动能是多少？
在离地20m高处，将一个质量为m=0.8kg的小球从离墙10m远处向墙平抛出去，在墙上落点B离地15m高.球经墙反弹后落地点D离墙8m远，求墙对球的冲量大小．球受墙作用力所做的功的大小．(g取10m/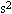
)
在纳米技术中需要移动或修补原子，必须使在不停地做热运动(速率约几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间，为此已发明了“激光致冷”技术．若把原子和入射光子分别类比为一辆小车和一个小球，则“激光致冷”与下述的模型很类似．
一辆质量为m的小车(一侧固定一轻弹簧)，如图所示，以速度v0水平向右运动，一动量大小为p，质量可以忽略的小球水平向左射入小车并压缩弹簧至最短，接着被锁定一定时间ΔT，再解除锁定使小球以大小相同的动量p水平向右弹出，紧接着不断重复上述过程，最终小车将停下来．设地面和车厢均为光滑，除锁定时间ΔT外．不计小球在小车上运动和弹簧压缩、伸长的时间，求：
(1)小球第一次入射后再弹出时，小车的速度的大小和这一过程中小车动能的减少量；
(2)从小球第一次入射开始到小车停止运动所经历的时间．
如图所示，固定在轻质弹簧两端，质量分别是
=0.5kg,
=1.49kg的两个物体，置于光滑水平面上,靠在光滑竖直墙上．现有一个m=0.01kg的子弹水平射入中(没有穿出)，使弹簧压缩而具有12J的弹性势能，再后
都将向右运动，试求：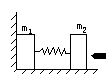
(1)子弹入射前的速度v；
(2)竖直墙对的冲量．
(3)运动过程中弹簧可具有的最大弹性势能．
质量为为M的小车静止在光滑水平面上，车的右侧面是由一个半径为R的
圆弧曲面和平面相连接，其平面离地高度为h，有一个质量为m的小球，从车顶A点上方H处自由下落，如图，经M车的平台右端C点抛出，问m球落地点离C点的水平距离多远？（一切摩擦均不计）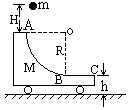
如图所示，一个质量为m的小玩具蛙，蹲在质量为M的小车的细杆上，小车静止在光滑的水平桌面上．若车长为L，竖直细杆顶端距小车平台高为h，且细杆底端正好位于平台中心．试求：当玩具蛙至少以多大的水平速度v跳出时，才能落到桌面上? 这一过程中，玩具蛙至少做多少功?(当地的重力加速度g)