某市规定卡车在市区一特殊路段行驶速度不得超过36km/h,有一辆卡车在危急情况下紧急刹车,车轮抱死滑动一段距离后停住,交警测得刹车过程中轮胎在路面上擦过的笔直的痕迹长9m,从厂家的技术手册中查得该车轮和地面的动摩擦因数为0.8。
(1)请你判断此辆卡车是否违反规定超速行驶(假定刹车后卡车做匀减速运动,计算时可取g = 10m/s2)
(2)如果汽车安装车轮防抱死装置,则紧急刹车时可获得比车轮抱死时更大的制动力,从而使刹车距离大大减小,而减小刹车距离则是避免交通事故的最有效途径,刹车距离除与汽车的初速度、制动力有关外,还必须考虑驾驶员的反应时间(司机从发现情况到肌肉动作操作制动器的时间),假设汽车安装办轮防抱死装置后刹车时的制动力是定值f,驾驶员的反应时间为t0,汽车的质量为m,行驶速度为v0,请你通过计算刹车距离并说明高速公路上严禁超速、超载和酒后驾驶的原因。
如图所示,两根光滑的长直金属导轨 MN、PQ平行置于同一水平面内,导轨间距L=0.2m,导轨左端接有“0.8V,0.8W’’的小灯泡,导轨处于磁感应强度为B=1T、方向竖直向下的匀强磁场中。长度也为L的金属导体棒ab垂直于导轨放置,导轨与导体棒每米长度的电阻均为R0=0.5Ω,其余导线电阻不计。今使导体棒在外力作用下与导轨良好接触向右滑动产生电动势,使小灯泡能持续正常发光。
(1)写出ab的速度v与它到左端MP的距离x的关系式,并求导体棒的最小速度vmin;
(2)根据v与x的关系式,计算出与表中x各值对应的v的数值填入表中,然后画出v-x图线。

如图所示,用长为L不可伸长的细线连结质量为m的小球,绳的O端固定,另用细线AB将小球拉起使细线OA与水平成30°角.现将AB线从A处剪断.
求:(1)剪断细线AB的瞬间小球的加速度;
(2)求剪断细线AB后小球下落至OA在水平线下方的对称位置OA/时的速度大小和方向
(3)求小球落到最低点时细线L中的拉力大小.
在xoy平面内,第Ⅲ象限内的直线OM是电场与磁场的边界,OM与负x轴成45°角。在x<0且OM的左侧空间存在着负x方向的匀强电场E,场强大小为32N/C,在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场B,磁感应强度大小为0.1T,如图(13)所示。一不计重力的带负电的微粒,从坐标原点O沿y轴负方向以υ0=2×103m/s的初速度进入磁场,已知微粒的带电量为q=5×10-18C,质量为m=1×10-24kg,(不计微粒所受重力),求:
(1)带电微粒第一次经过磁场边界的位置坐标;
(2)带电微粒在磁场区域运动的总时间;
(3)带电微粒最终离开电、磁场区域的位置坐标。
如图(12)所示,挡板P固定在足够高的水平桌面上,小物块A和B大小可忽略,它们分别带有+QA和+QB的电荷量,质量分别为mA和mB。两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过滑轮,一端与B连接,另一端连接一轻质小钩.整个装置处于场强为E、方向水平向左的匀强电场中。A、B开始时静止,已知弹簧的劲度系数为k,不计一切摩擦及A、B间的库仑力,A、B所带电荷量保持不变,B不会碰到滑轮。
(1)若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力恰为零,但不会离开P,求物块C下降的最大距离;
(2)若C的质量改为2M,则当A刚离开挡板P时,B的速度多大?
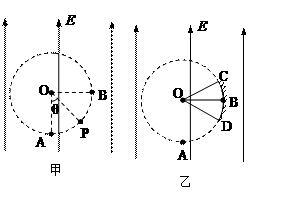
如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是最右侧的点。在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电量为q,不计重力。试求:
(1)电荷在电场中运动的加速度多大?
(2)运动轨迹经过B点的电荷在A点时的速度多大?
(3)某电荷的运动的轨迹和圆形区域的边缘交于P点,∠POA=θ,请写出该电荷经过P点时动能的表达式。
(4)若在圆形区域的边缘有一接收屏CBD,C、D分别为接收屏上最边缘的两点,如图乙,∠COB=∠BOD=30°。求该屏上接收到的电荷的末动能大小的范围。