如图所示，矩形区域MNPQ内有水平向右的匀强电场，虚线框外为真空区域；半径为R、内壁光滑、内径很小的绝缘半圆管ADB固定在竖直平面内，直径AB垂直于水平虚线MN，圆心O恰在MN的中点，半圆管的一半处于电场中．一质量为m，可视为质点的带正电电荷量为q的小球从半圆管的A点由静止开始滑入管内，小球从B点穿出后，能够通过B点正下方的C点．重力加速度为g，小球在C点处的加速度大小为5 g/3．求：
（1）匀强电场场强E；
（2）小球在B点时，半圆轨道对它作用力的大小；
（3）要使小球能够到达B点正下方C点，虚线框MNPQ的高度和宽度满足什么条件；
（4）小球从B点计时运动到C点过程中，经多长时间小球的动能最小.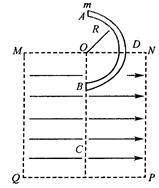
做“双缝干涉测光的波长”实验时，如果用白光照射双缝，屏上干涉条纹的中央亮纹是色的，共它各级条纹中最外侧的条纹是色的．
一种红宝石激光器发射的激光是不连续的一道道闪光，每道闪光称为—个光脉冲．若这种激光器光脉冲的持续时间为1.0×10-11
，波长为694。3nm，发射功率为1.0×lO10W，问(1)每列光脉冲的长度是多少?(2)用红宝石激光器照射皮肤上色斑，每l0mm2色斑上吸收能量达到60J以后，便逐渐消失．一颗色斑的面积为50mm2，则要吸收多少个红宝石激光脉冲，才能逐渐消失?
—束光由真空射到平面玻璃上，当其折射角为30º时，反射光恰好产生完全偏振，试求玻璃的折射率．
两个动能均为1Mev的氘核发生正面碰撞，引起了如下的核反应:
试求:
①此核反应中放出的能量ΔΕ 等于多少?
②若放出的能量全部变成核的动能，则生成的氢核具有的动能是多少?（已知
、
、
的原子核的质量分别为1.0073u、2.0136u 、3.0156u）
两个氘核聚变产生一个中子和一个氦核（氦的同位素），若在反应前两个氘核的动能均为
，它们正面碰撞发生核聚变，且反应后释放的能量全部转化为动能，反应后所产生的中子的动能为2.49MeV，求该核反应所释放的核能。已知氘核的质量为
，氦核的质量为
，中子的质量为
。