如图所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN。导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻。有一匀强磁场垂直于导轨平面,磁感强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计。现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行。已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=1m。试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
(1)当金属棒滑行至cd处时回路中的电流多大?
(2)金属棒达到的稳定速度是多大?
(3)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感强度逐渐减小,可使金属棒中不产生感应电流,则t=1s时磁感应强度应为多大?
为了保证行车安全,不仅需要车辆有良好的刹车性能,还需要在行车过程中前后车辆保持一定的距离.驾驶手册规定,在一级公路上,允许行车速度为υ1,发现情况后需在S1距离内被刹住.在高速公路上,允许行车速度为υ2(υ2>υ1),发现情况后需在S2(S2>S1)距离内被刹住。假设对于这两种情况驾驶员允许的反应时间(发现情况到开始刹车经历的时间)与刹车后的加速度都相等,求允许驾驶员的反应时间和刹车加速度.
用同种材料制成倾角30°的斜面和长水平面,斜面长2.4m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0="2" m/s时,经过0.8s后小物块停在斜面上。多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象,如图所示,求:
1)小物块与该种材料间的动摩擦因数为多少?
2)某同学认为,若小物块初速度为4m/s,则根据图象中t与v0成正比推导,可知小物块运动时间为1.6s。以上说法是否正确?若不正确,说明理由并解出你认为正确的结果。
科研人员乘气球进行科学考察.气球、座舱、压舱物和科研人员的总质量为990 kg.气球在空中停留一段时间后,发现气球漏气而下降,及时堵住.堵住时气球下降速度为1 m/s,且做匀加速运动,4 s内下降了12 m.为使气球安全着陆,向舱外缓慢抛出一定的压舱物.此后发现气球做匀减速运动,下降速度在5分钟内减少3 m/s.若空气阻力和泄漏气体的质量均可忽略,重力加速度g=9.89 m/s2,求抛掉的压舱物的质量.
“神舟”六号飞船完成了预定空间科学和技术试验任务后,返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回,在离地10km的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k,设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落。从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点C的坐标为(0,8)。g=10m/s2,请解决下列问题:
(1)在初始时刻v0=160m/s时,它的加速度多大?
(2)推证空气阻力系数k的表达式并算出其数值。
(3)返回舱在距离高度h=1m时,飞船底部的4个反推力小火箭点火工作,使其速度由8m/s迅速减至1m/s后落在地面上,若忽略燃料质量的减少对返回舱总质量的影响,并忽略此阶段速度变化而引起空气阻力的变化,试估算每支小火箭的平均推力(计算结果取两位有效数字)
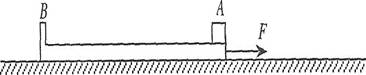
如图所示,质量M=4kg的木板B静止于光滑的水平面上,其左端带有挡板,上表面长L=1m,木板右端放置一个质量m=2kg的木块A(可视为质点),A与B之间的动摩擦因素μ=0.2。现在对木板B施加一个水平向右的恒力F=14N,使B向右加速运动,经过一段时间后,木块A将与木板B左侧的挡板相碰撞,在碰撞前的瞬间撤去水平恒力F。已知该碰撞过程时间极短且无机械能损失,假设A、B间的最大静摩擦力跟滑动摩擦力相等,g取10m/s2。,试求:
(1)撤去水平恒力F的瞬间A、B两物体的速度大小vA、VB分别多大
(2)此过程F所做的功;
(3)撤去水平恒力F前因摩擦产生的热量。