图甲所示为回旋加速器的原理示意图，一个扁圆柱形的金属盒子，盒子被分成两半（D形电极），分别与高压交变电源的两极相连，在裂缝处形成一个交变电场，高压交流电源的U－t图象如图乙所示，图中U（×104V），t (×10－7s)，在两D形电极裂缝的中心靠近其中一个D形盒处有一离子源Ｋ，D形电极位于匀强磁场中，磁场方向垂直于D形电极所在平面，由下向上。从离子源K发出的氘核，在电场作用下，被加速进入盒中．又由于磁场的作用，沿半圆形的轨道运动，并重新进入裂缝。这时恰好改变电场方向，氘核在电场中又一次加速，如此不断循环进行，最后在D形盒边缘被特殊装置引出。（忽略氘核在裂缝中运动的时间）
（1）写出图乙所示的高压交流电源的交流电压瞬时值的表达式；
（2）将此电压加在回旋加速器上，给氘核加速，则匀强磁场的磁感强度应为多少?
（3）若要使氘核获得5.00MeV的能量，需要多少时间?（设氘核正好在电压达到峰值时通过D形盒的狭缝）
（4）D形盒的最大半径R。
如图所示，A、B两个矩形木块用轻弹簧相接静止在水平地面上，弹簧的劲度系数为k，木块A和木块B的质量均为m．
（1）若用力将木块A缓慢地竖直向上提起，木块A向上提起多大高度时，木块B将离开水平地面．
（2）若弹簧的劲度系数k是未知的，将一物体C从A的正上方某位置处无初速释放，C与A相碰后立即粘在一起（不再分离）向下运动，它们到达最低点后又向上运动．已知C的质量为m时，把它从距A高为H处释放，则最终能使B刚好离开地面．若C的质量为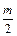
，要使B始终不离开地面，则释放时，C距A的高度h不能超过多少？
如图所示，滑块A1A2由轻杆连结成一个物体，其质量为M，轻杆长L．滑块B的质量为m，长L/2，其左端为一小槽，槽内装有轻质弹簧．开始时，B紧贴A，使弹簧处在压缩状态．今突然松开弹簧，在弹簧作用下整个系统获得动能Ek，弹簧松开后，便离开小槽并远离物体A1A2．以后B将在A1和A2之间发生无机械能损失的碰撞．假定整个系统都位于光滑的水平面上，求物块B的运动周期．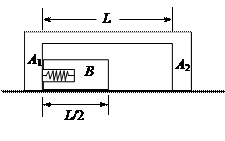
如图所示，质量M为4kg的平板小车静止在光滑的水平面上，小车左端放一质量为lkg的木块，车的右端固定一个轻质弹簧．现给木块一个水平向右的10N·s的瞬间冲量，木块便沿车向右滑行，在与弹簧相碰后又沿原路返回，并恰好能达到小车的左端，求：
（1）弹簧被压缩到最短时平板车的速度v；
（2）木块返回小车左端时的动能Ek；
（3）弹簧获得的最大弹性势能Epm．
如图所示，EF为水平地面，O点左侧是粗糙的，右侧是光滑的，一轻质弹簧右端固定在墙壁上，左端与静止在O点、质量为m的小物块A连接，弹簧处于原长状态．质量为2m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动，已知物块B与地面EO段间的滑动摩擦力大小为
，物块B运动到O点与物块A相碰并一起向右运动（设碰撞时间极短），运动到D点时撤去外力F．物块B和物块A可视为质点．已知CD=5L，OD=L．求：
（1）撤去外力后弹簧的最大弹性势能?
（2）物块B从O点开始向左运动直到静
止所用的时间是多少?
如图所示，劲度系数为k=200N/m的轻弹簧一端固定在墙上，另一端连一质量为M=8kg的小车a，开始时小车静止，其左端位于O点，弹簧没有发生形变，质量为m=1kg的小物块b静止于小车的左侧，距O点s=3m，小车与水平面间的摩擦不计，小物块与水平面间的动摩擦系数为μ=0.2，取g=10m/s2．今对小物块施加大小为F=8N的水平恒力使之向右运动，并在与小车碰撞前的瞬间撤去该力，碰撞后小车做振幅为A=0.2m的简谐运动，已知小车做简谐运动周期公式为T=2
，弹簧的弹性势能公式为Ep=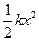
（x为弹簧的形变量），求：
（1）小物块与小车磁撞前瞬间的速度是多大？
（2）小车做简谐运动过程中弹簧最大弹性势能是多少？小车的最大速度为多大？
（3）小物块最终停在距O点多远处？当小物块刚停下时小车左端运动到O点的哪一侧？