如图所示，建立xOy坐标系，两平行极板P、Q垂直于y轴且关于x轴对称，极板长度和板间距均为l，两板间电压大小为U；第一、四象限有磁感应强度为B的匀强磁场，方向垂直于xOy平面向里。位于极板左侧的粒子源沿x轴向右发射一个质量为m、电量为+q、重力不计的带电粒子，带电粒子恰好经极板边缘射入磁场。上述m、q、l、U、B为已知量。（不考虑极边缘的影响）。求
（1）粒子从粒子源射出时的速度大小。
（2）带电粒子在磁场中做圆周运动的半径和周期。
如图所示，abcde和a'b'c'd'e'为两平行的光滑导轨，其中abcd和a'b'c'd'部分为处于水平面内的直轨，ab、a'b'的间距为cd、c'd'间距的2倍；de和d'e'部分为与直轨相切的、半径均为R的半圆形轨道，处于竖直平面内．直轨部分处于竖直向上的匀强磁场中，弯轨部分处于匀强磁场外．在靠近aa'和cc'处放有两根金属棒MN、PQ，质量分别为2m和m．为使棒PQ能沿导轨运动并通过半圆形轨道的最高点ee'，在初始位置必须至少给棒MN以多大的冲量?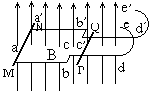
(设两段水平直轨均足够长，棒PQ出磁场时MN仍在宽轨道上运动)
如图所示，质量为m=0.1kg的铝框，用绝缘细线悬挂起来，框中心距地面高h=0.8m，有一质量M=0.2kg的磁铁以10m/s的水平速度沿框中心穿过铝框，落在距铝框原位置水平距离s=3.6m处，则在磁铁与铝框发生相互作用时：
(1)铝框向哪边偏转?它能上升多高?
(2)在磁铁穿过铝框过程中，框中产生多少电能?
在光滑水平地面上，两根彼此平行的光滑导轨PQ、MN相距为L=1m，在它们的末端垂直PQ、MN跨放一金属杆ab，ab的质量为m=0.005kg，在导轨的另一端连接一个已经充电的电容器，电容器的电容C=200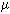
F，有一匀强磁场，方向垂直导轨PQ、MN所在平面向下，如图所示，磁感强度为B=0.5T．(除导轨PQ、MN和金属杆ab外其余部分都是绝缘的)当闭合电键K时，ab杆将从导轨上冲出，并沿光滑斜面升到高为0.2m处，这过程电容器两端电压减小了一半，求：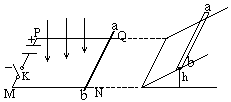
(1)磁场对金属杆ab冲量的大小．
(2)电容器原来充电电压是多少．
如图所示，由电磁感应现象形成的电源和平行板电容器相连接。电源内有固定的25匝线圈，穿过线圈的磁通量Φ随时间t变化规律如(b)图。平行板电容器两个极板水平放置，板间距离d=2cm．两极板间有一个带电微粒，质量m=1.0×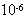
kg，带负电。电量为q=1.8×
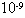C．假设t=0时，上极板电势高，且此时带电微粒的即时速度为零，假定带电微粒的运动不会碰到极板。试求：
(1)微粒所受电场力是它重力的多少倍？
(2)微粒在30ms末的瞬时速度。
(3)微粒在30ms末相对于起始位置的位移。
如图所示，总质量是m的闭合线圈，静止于水平支持面上，有一狭长水平导轨垂直穿过此线圈．现有一质量为m的条形磁铁，沿导轨通过线圈．已知磁铁进入线圈前的动能为
，离开线圈时的动能为
．若各处的摩擦力都不计，试计算磁铁通过线圈时共产生多少热量．