如图所示，ABC是竖直固定的半圆形光滑圆弧槽，底端与水平地面相切于C点，半径R=0.1m．P、Q是两个可视为质点的物体，
、
5kg，其间放有一压缩弹簧，且P开始静止于D处．P、Q与水平地面的摩擦因素均为μ=0.5，某时刻弹簧将P、Q瞬间水平推开（不考虑推开过程中摩擦力的影响），有E=15J的弹性势能转化为P、Q
的动能．（g取10m／s2）
求：（1）P、Q被推开瞬间各自速度的大小?
（2）当CD间距离S1满足什么条件时，P物体可到达槽最高点A。
在天体运动中，将两颗彼此距离较近，且相互绕行的行星称为双星。已知两行星质量分别为M1和M2，它们之间距离为L，求各自运转半径和角速度为多少？
阅读下列材料，并结合材料解题
开普勒从1909年——1919年发表了著名的开普勒行星三定律：
第一定律：所有的行星分别在大小不同的椭圆轨道上绕太阳运动，太阳在这个椭圆的一个焦点上
第二定律：太阳和行星的连线在相等的时间内扫过相等的面积
第三定律：所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等
实践证明，开普勒三定律也适用于人造地球卫星的运动，如果人造地球卫星沿半径为r的圆形轨道绕地球运动，当开动制动发动机后，卫量速度降低并转移到与地球相切的椭圆轨道，如图问在这之后，卫星经过多长时间着陆？空气阻力不计，地球半径为R，地球表面重力加速度为g，圆形轨道作为椭圆轨道的一种特殊形式。
宇宙飞船以a=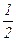
g=5m/s2的加速度匀速上升，由于超重现象，用弹簧秤测得质量为10kg的物体重量为75N，由此可求飞船所处位置距地面高度为多少？(地球半径R=6400km)
地核体积约为地球体积的16%，地球质量约为地球质量的34%，引力常量取G=6.7×10－11Nm2/kg2，地球半径取R=6.4×106m，地球表面重力加速度取g=9.8m/s2，试估算地核的平均密度(结果取2位有效数字)。
如图30-1所示，虚线上方有场强为E的匀强电场，方向竖直向下，虚线上下有磁感强度相同的匀强磁场，方向垂直纸面向外。ab是一根长L的绝缘细杆，沿电场线放置在虚线上方的场中，b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后，小球先是加速运动，后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3，小球的重力可忽略不计。当小球脱离杆进入虚线下方后，运动轨迹是半圆，圆半径为L/3。求：带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。