如图6—8—23所示,杆长为L,杆的一端固定一质量为m的小球,杆的质量忽略不计,整个系统绕杆的另一端O在竖直平面内作圆周运动,求:
(1)小球在最高点A时速度 为多大时,才能使杆对小球m的作用力为零?
为多大时,才能使杆对小球m的作用力为零?
(2)小球在最高点A时,杆对小球的作用力F为拉力和推力时的临界速度是多少?
(3)如m =" 0.5kg," L =" 0.5m,"  =" 0.4m/s," 则在最高点A和最低点B时, 杆对小球m的作用力各是多大? 是推力还是拉力?
=" 0.4m/s," 则在最高点A和最低点B时, 杆对小球m的作用力各是多大? 是推力还是拉力?
如图12-2-6所示,半径为R、单位长度电阻为λ的均匀导体圆环固定在水平面上,圆环中心为O.匀强磁场垂直水平面方向向下,磁感强度为B.平行于直径MON的导体杆,沿垂直于杆的方向向右运动.杆的电阻可以忽略不计,杆与圆环接触良好,某时刻,杆的位置如图, ,速度为v,求此时刻作用在杆上安培力的大小.
,速度为v,求此时刻作用在杆上安培力的大小.
如图12-2-4所示,在磁感强度为B的匀强磁场中有一半径为L的金属圆环.已知构成圆环的电线电阻为4r0,以O为轴可以在圆环上滑动的金属棒OA电阻为r0,电阻R1=R2=4r0.当OA棒以角速度 匀速转动时,电阻R1的电功率最小值为P0为多大?(其它电阻不计)
匀速转动时,电阻R1的电功率最小值为P0为多大?(其它电阻不计)
如图12-2-11(a)所示,一端封闭的两条平行光滑导轨相距L,距左端L处的中间一段被弯成半径为H的1/4圆弧,导轨左右两段处于高度相差H的水平面上.圆弧导轨所在区域无磁场,右段区域存在磁场B0,左段区域存在均匀分布但随时间线性变化的磁场B(t),如图12-2-11(b)所示,两磁场方向均竖直向上.在圆弧顶端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路,从金属棒下滑开始计时,经过时间t0滑到圆弧底端.设金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g.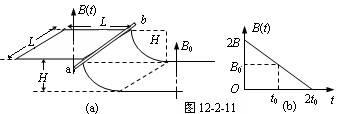
(1)问金属棒在圆弧内滑动时,回路中感应电流的大小和方向是否发生改变?为什么?
(2)求0到时间t0内,回路中感应电流产生的焦耳热量.
(3)探讨在金属棒滑到圆弧底端进入匀强磁场B0的一瞬间,回路中感应电流的大小和方向.
质量m=1kg的小车左端放有质量M=3kg的铁块,两者以v0=4m/s的共同速度沿光滑水平面向竖直墙运动,车与墙的碰撞时间极短,无动能损失。铁块与车间的动摩擦因数为μ=1/3,车足够长,铁块不会到达车的右端。从小车第一次与墙相碰开始计时,取水平向右为正方向,g=10m/s2,求:(1)当小车和铁块再次具有共同速度时,小车右端离墙多远?(2)在答卷的图上画出第二次碰撞前,小车的速度时间图象。不要求写出计算过程,需在图上标明图线的起点、终点和各转折点的坐标。
某同学在地面上将质量为m的一物块以初速度V 竖直向上抛出,经过
竖直向上抛出,经过 时间,物块以速率
时间,物块以速率 落回该同学手中。物块运动的
落回该同学手中。物块运动的 -t图如下,求
-t图如下,求
(1)物块上升的最大高度;
(2)物块运动过程中所受空气阻力大小。