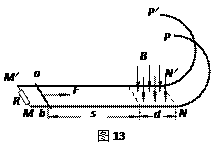
如图13所示，两根正对的平行金属直轨道MN、M′N′位于同一水平面上，两轨道之间的距离l=0.50m。轨道的MM′端之间接一阻值R=0.40Ω的定值电阻，NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接，两半圆轨道的半径均为R0=0.50m。直轨道的右端处于竖直向下、磁感应强度B=0.64 T的匀强磁场中，磁场区域的宽度d=0.80m，且其右边界与NN′重合。现有一质量m=0.20kg、电阻r=0.10Ω的导体杆ab静止在距磁场的左边界s=2.0m处。在与杆垂直的水平恒力F=2.0N的作用下ab杆开始运动，当运动至磁场的左边界时撤去F，结果导体杆ab恰好能以最小速度通过半圆形轨道的最高点PP′。已知导体杆ab在运动过程中与轨道接触良好，且始终与轨道垂直，导体杆ab与直轨道之间的动摩擦因数μ=0.10，轨道的电阻可忽略不计，取g=10m/s2，求：
（1）导体杆刚进入磁场时，通过导体杆上的电流大小和方向；
（2）导体杆穿过磁场的过程中通过电阻R上的电荷量；
（3）导体杆穿过磁场的过程中整个电路中产生的焦耳热。
（1）（本小题共3分，在给出的四个选项中，可能只有一个选项正确，也可能有多个选项正确，全部选对得3分，选对但不全的得1分，有错选的得0分）
在下列说法中，正确的是（）
A．物体的的温度升高了l℃，用热力学温标表示就是升高了1K
B．“酒香不怕巷子深”是与分子热运动有关的现象
C．已知气体的摩尔质量、密度及阿伏加德罗常数．就可以估算出该气体分子的直径
D．用油膜法估测分于直径实验中．计算结果明显偏人，可能是由于油酸中含有人量的酒精
（2）（本小题共3分，在给山的四个选项中，可能只有一个选项正确，也可能有多个选项正确，全部选对得3分，选对但不全的得1分，有错选的得0分）
关于热现象，下列说法中正确的是（）
A．热现象过程中不可避免地会出现能量耗散现象
B．凡是不违背能量守恒定律的实验构想，都是能够实现的
C．任何自然过程不一定总是沿着熵增加的方向进行
D．电冰箱即使在工作时，也不可能把箱内低温物体的热越传到箱外高温物体
（3）（本小题共4分）
如图所所示的圆柱形容器内用轻质活塞密封一定质量的理想气体。若活塞固定，密封气体温度升高1℃，需吸收的热量为Q1；若活塞不固定，且可无摩擦滑动，仍使密封气体温度升高1℃，需吸收的热量为Q2，问Q1与Q2哪个大？简要说明理由。
（1）小球飞离D点时的速度；
（2）小球从B点到D点过程中克服摩擦所做的功
（3）小球再次进入圆管后，能否越过C点？请分析说明理由。
（1）滑板与斜面间的动摩擦因数
；
（2）运动员能滑上斜面的最大高度h
（1）带电微粒从电场中射出时的速度大小和方向；
（2）带电微粒进入中间三角形区域后，要垂直打在AC边上，则该区域的磁感应强度B1是多少？
（3）确定微粒最后出磁场区域的位置。
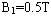
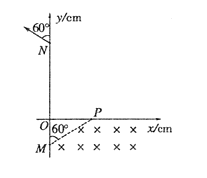
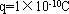的带正电微粒，以某一初速度v沿与y轴正方向成60°角从M点进入第四象限后沿直线运动，在P点进入处于第一象限内的磁场B2区域。一段时间后，微粒经过y轴上的N点并以与y轴正方向成60°角飞出。M点的坐标为（0，—10），N点的坐标为（0，30），不计微粒重力，g取10m/s2。
（1）请分析判断匀强电场E的方向并求出微粒的速度大小；
（2）匀强磁场B2的大小为多大？
（3）B2磁场区域的最小面积为多少？