利用如图7所示的装置测量滑块和滑板间的动摩擦因数。将质量为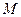 的滑块
的滑块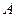 放在倾斜滑板
放在倾斜滑板 上,
上,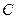 为位移传感器,它能将滑块
为位移传感器,它能将滑块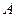 到传感器
到传感器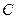 的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示出滑块
的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示出滑块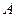 的速度——时间(
的速度——时间(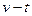 )图像。先给滑块
)图像。先给滑块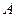 一个沿滑板
一个沿滑板 向上的初速度,得到的
向上的初速度,得到的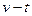 如图8所示,求:
如图8所示,求:
(1)滑块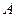 上滑时加速度的大小;
上滑时加速度的大小;
(2)滑块与滑板之间的动摩擦因数(取重力加速度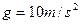 )。
)。
如图所示,用质量为m、电阻为R的均匀导线做成边长为l的单匝正方形线框MNPQ,线框每一边的电阻都相等。将线框置于光滑绝缘的水平面上。在线框的右侧存在竖直方向的有界匀强磁场,磁场边界间的距离为2l,磁感应强度为B。在垂直MN边的水平拉力作用下,线框以垂直磁场边界的速度v匀速穿过磁场。在运动过程中线框平面水平,且MN边与磁场的边界平行。求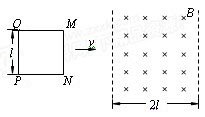
(1)线框MN边刚进入磁场时,线框中感应电流的大小;
(2)线框MN边刚进入磁场时,M、N两点间的电压UMN;
(3)在线框从MN边刚进入磁场到PQ边刚穿出磁场的过程中,水平拉力对
线框所做的功W。
1789年英国著名物理学家卡文迪许首先估算出了地球的平均密度。根据你学过的知识,能否知道地球平均密度的大小。
中子星是恒星演变到最后的一种存在形式.
(1)有一密度均匀的星球,以角速度ω绕自身的几何对称轴旋转.若维持其表面物质不因快速旋转而被甩掉的力只有万有引力,那么该星球的密度至少要多大?
(2)蟹状星云中有一颗中子星,它每秒转30周,以此数据估算这颗中子星的最小密度.
(3)若此中子星的质量约为太阳的质量(2×1030 kg),试问它的最大可能半径是多大?
(1)试在图中粗略画出恒星运动的轨道和位置;
(2)试计算恒星与点C间的距离和恒星的运行速率v.
我国预计在2007年4月份发射一颗绕月运行的探月卫星“嫦娥1号”。设“嫦娥1号”卫星环绕月球做圆周运动,并在此圆轨道上绕行n圈,飞行时间为t。已知月球半径为R,月球表面的重力加速度为g。导出飞船在上述圆轨道上运行时离月球表面高度h的公式(用t、n、R、g表示)