已知数列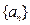 中,
中,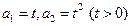 。
。
若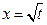 是函数
是函数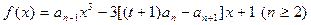 的一个极值点。
的一个极值点。
(1)求数列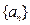 的通项公式;
的通项公式;
(2)若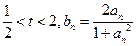 ,求证:对于任意正整数
,求证:对于任意正整数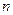 ,
,
都有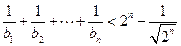 ;
;
(3)若 ,证明:
,证明: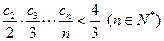
已知等比数列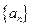 ,
,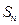 是其前
是其前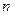 项的和,且
项的和,且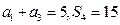 .
.
(1)求数列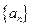 的通项公式;
的通项公式;
(2)设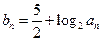 ,求数列
,求数列 的前
的前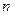 项和
项和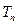 ;
;
甲、乙两个篮球运动员相互没有影 响地站在罚球线上投球,其中甲的命中率为
响地站在罚球线上投球,其中甲的命中率为 ,乙的命中率为
,乙的命中率为 ,现在每人都投球三次,且各次投球的结果互不影响.求:
,现在每人都投球三次,且各次投球的结果互不影响.求:
(1)甲恰好投进两球 的概率
的概率 ;
;
(2)甲乙两人都恰好投进两球的概率;
已知向量
(1)求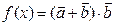 的值域;
的值域;
(2)求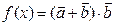 在
在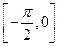 上的值域.
上的值域.
如图, 是双曲线C的两个焦点,直线
是双曲线C的两个焦点,直线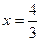 是双曲线C的右准线.
是双曲线C的右准线.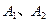 为双曲线C的两个顶点,点P是双
为双曲线C的两个顶点,点P是双 曲线C右支上异于
曲线C右支上异于 的一动点,直线
的一动点,直线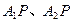 交双曲线C的右准线分别为
交双曲线C的右准线分别为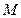 、
、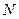 两点.
两点.
⑴求双曲线C的方程;
⑵求证: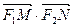 为定值.
为定值.