质量为m的小球固定在光滑轻细杆的上端，细杆通过光滑限位孔保持竖直。在光滑水平面上放置一质量为M＝2m的凹形槽，凹形槽的光滑内表面如图所示，AB部分是斜面，与水平面成θ＝30°，BCD部分是半径为R的圆弧面，AB与BCD两面在B处相切。让细杆的下端与凹形槽口的左边缘A点接触。现将小球释放，求：
（1）当轻细杆的下端滑到凹形槽的最低点C时，凹形槽的速度是多大；
（2）轻细杆的下端能否运动到凹形槽口的右边缘D点；（只要回答“能”或“不能”，不需说明原因）
（3）当轻细杆的下端滑到B点的瞬间，小球和凹形槽的速度各是多大。
（1）某运动员吸一口气，吸进400cm
的空气，据此估算他所吸进的空气分子的总数。已知1mol气体处于标准状态时的体积是22.4L。（结果保留一位有效数字）
（2）如图所示，绝热隔板S把绝热的气分隔成体积相等的两部分，S与气缸壁的接触是光滑的。两部分中分别盛有相同质量、相同温度的同种气体
和
，气体分子之间相互作用可忽略不计。现通过电热丝对气体缓慢加热一段时间后，
各自达到新的平衡状态。试分析气体的压强、温度、内能的变化情况。
相距为L的两光滑平行导轨与水平面成θ角放置。上端连接一阻值为R的电阻，其余电阻不计．整个装置处在方向竖直向上的匀强磁场中，磁感强度为B，质量为m、电阻为r的导体MN垂直导轨放在导轨上，如图所示。现由静止释放导体MN，求：
（1）MN可达的最大速度vm；
（2）当MN速度v=vm/3时的加速度a；
（3）回路产生的最大电功率Pm．
如图所示，a、b是两相距L＝0.5m的平行、光滑的水平金属导轨，在其上垂直放置两根金属杆1和2，其质量分别为m1＝0.1kg，m2＝0.2kg，电阻分别为R1＝1Ω，R2＝0.25Ω，B＝1.2T的匀强磁场竖直向下，a、b两导轨电阻忽略不计．现对2棒施以水平向右的极短时间的打击力作用，使其获得大小为1N·s的冲量．求此后：
（1）1棒运动的最大加速度和最大速度；
（2）回路所产生的电能．
发电站发电机端电压u＝5000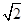
sin314tV，输出功率5000kW，远距离输电线的电阻为80Ω，输电线上功率损耗要求不超过总功率的4%，求:
(1)所用升压变压器的原、副线圈匝数比多大?
(2)到达用户区使用匝数比为192：1的降压变压器，对负载电阻为10Ω的用电器供电，最多可接这样的用电器几个?
如图所示，线圈abcd的面积是0.05m2，共100匝，线圈电阻1Ω，外接电阻R＝9Ω，匀强磁场的磁感应强度为B＝
T．线圈在外力作用下以300r/s的转速匀速转动．求：
（1）若从线圈处于中性面开始计时，写出线圈中感应电动势的瞬时值表达式．
（2）电路中电流表的示数是多少？
（3）线圈从图示状态转过90°通过线圈横截面的电荷量．