我国的“嫦娥奔月”月球探测工程已经启动，分“绕、落、回”三个发展阶段：在2007年已经发射了一颗围绕月球飞行的“嫦娥一号”卫星，将在2012年前后发射一颗月球软着陆器，在2017年前后发射一颗返回式月球软着陆器，进行首次月球样品自动取样并安全返回地球.设想着陆器完成了对月球表面的考察任务后，由月球表面回到围绕月球做圆周运动的轨道舱，如图19所示.为了安全，返回的着陆器与轨道舱对接时，必须具有相同的速度。设返回的着陆器质量为m，月球表面的重力加速度为g，月球的半径为R，月球的自转周期为T，轨道舱到月球中心的距离为r，已知着陆器从月球表面返回轨道舱的过程中需克服月球引力做功
，不计月球表面大气对着陆器的阻力和月球自转的影响，则
（1）着陆器与返回舱对接时的速度大小是多少？
（2）在月球表面的着陆器至少需要获得多少能量才能返回轨道舱？
导体棒OA垂直磁感线放置，如图所示，已知匀强磁场的磁感强度为B(T)，OA长为L(m)，OA棒绕O点匀速转动，转速为n(r/s)，推导OA棒在匀速转动中的感应电动势
图是最早的简易发电机──法拉第圆盘发电机．A为铜盘，OO'为转轴，磁感线穿过圆盘，圆盘在动力机带动下匀速转动时，轴与盘的边缘间产生电势差．若已知铜盘直径D=10cm，匀强磁场磁感强度B=1.0T，盘转速n="1800" r/min，计算盘转动时，发电机的感应电动势E的值．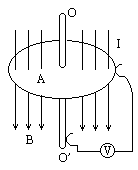
如图所示，一根粗金属棒MN固定放置，它的M一端连一个定值电阻R，定值电阻的另一端连接在金属轴O上．另外一根长为l的金属棒ab，a端与轴O相连，b端与MN棒上的一点接触，此时ab与MN间的夹角为45°角，如图所示．空间存在着方向垂直纸面向外的匀强磁场，磁感强度大小为B．现使ab棒以O为轴逆时针匀速转动一周，转动角速度大小为ω，转动过程中凡能与MN棒接触的都接触良好，两金属棒的电阻都可忽略不计．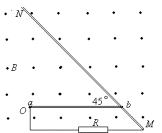
(1)写出电阻R中有电流存在的时间．
(2)写出这段时间内感应电流i随时间t变化的关系式．
(3)求出这段时间内流过电阻R的总电量．
如图所示，在磁感应强度为B的匀强磁场中，两根金属杆OM、ON在O点相接，夹角为120°。金属棒AC与两金属杆接触，接触点是E、F，△OEF是等腰三角形，EO=L。金属杆、金属棒单位长度的电阻都是K，现让AC以加速度a从静止开始垂直于AC向左运动，求回路中电功率的最大值。（已知磁场方向垂直△OEF所在平面）。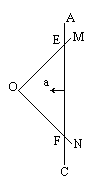
如图所示，水平放置的闭合圆形线圈，半径为a，磁场方向与线圈平面垂直．如果磁感强度的变化规律为B=Kt，线圈所用的导线截面积为b，导线的电阻率为ρ．求：在△t 时间内线圈所产生的热量．