(1)若输入腔中的电场保持不变，电子以一定的初速度v0从A板上的小孔沿垂直于A板的方向进入输入腔，而由B板射出输入腔时速度减为v0／2，求输入腔中的电场强度E的大小
(2)现将B板接地(图中未画出)，在输入腔的两极板间加上如图所示周期为T的高频方波交变电压，在t=0时A板电势为U0，与此同时电子以速度v0连续从A板上的小孔沿垂直A板的方向射人输入腔中，并能从B板上的小孔射出，射向输出腔的C孔．若在nT～(n+1)T的时间内(n=0，l，2，3…)，前半周期经B板射出的电子速度为v1，后半周期经B板射出的电子速度为v2，求v1与v2的比值。
如图5-9所示，半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm（β为待定系数）。A球从左边与圆心等高处由静止开始沿轨道下滑，与静止于轨道最低点的B球相撞，碰撞后A、B球能达到的最大高度均为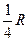
,碰撞中无机械能损失。重力加速度为g。试求：
（1）待定系数β;
（2）第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;
（3）小球A、B在轨道最低处第二次碰撞刚结束时各自的速度，并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度。
如图5-8所示，滑块A、B的质量分别为m1与m2，m1＜m2，由轻质弹簧相连接置于水平的气垫导轨上，用一轻绳把两滑块拉至最近，使弹簧处于最大压缩状态后绑紧。两滑块一起以恒定的速率v0向右滑动。突然轻绳断开，当弹簧伸至本身的自然长度时，滑块A的速度正好为0。求：
(1)绳断开到第一次恢复自然长度的过程中弹簧释放的弹性势能Ep；
(2)在以后的运动过程中，滑块B是否会有速度为0的时刻?试通过定量分析证明你的结论.
）如图5-7所示，坡道顶端距水平面高度为h，质量为m1的小物块A从坡道顶端由静止滑下，进入水平面上的滑道时无机械能损失，为使A制动，将轻弹簧的一端固定在水平滑道延长线M处的墙上，另一端与质量为m2的档板相连，弹簧处于原长时，B恰好位于滑道的末端O点。A与B碰撞时间极短，碰撞后结合在一起共同压缩弹簧。已知在OM段A、B与水平面间的动摩擦因数为μ，其余各处的摩擦不计，重力加速度为g，求
（1）物块A在档板B碰撞瞬间的速度v的大小；
（2）弹簧最大压缩时为d时的弹性势能EP（设弹簧处于原长时弹性势能为零）。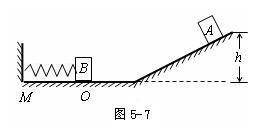
如图5-5所示，质量为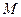
的天车静止在光滑轨道上，下面用长为
的细线悬挂着质量为
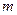的沙箱，一颗质量为
的子弹，以
的水平速度射入沙箱，并留在其中，在以后运动过程中，求：沙箱上升的最大高度。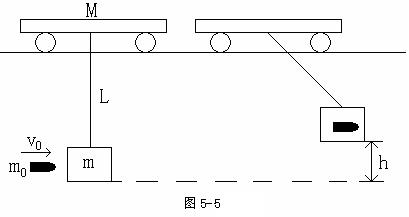
汽车进站关闭发动机做匀减速直线运动，当滑行s1＝300m时，速度恰好减为初速度的一半，接着又滑行了t2＝20s才停止．求：汽车滑行的总时间t，关闭发动机时的速度vo和总位移s．