、在学习了“实验:探究碰撞中的不变量”的实验后,得出了

动量守恒定律,反过来我们可以利用该实验中的有关方案来验证动量守恒定律。下面是某实验小组选用水平气垫导轨、光电门的测量装置来研究两个滑块碰撞过程中系统动量的变化情况。实验仪器如图所示。
实验过程:
(1)调节气垫导轨水平,并使光电计时器系统正常工作。
(2)在滑块1上装上挡光片并测出其长度L。
(3)在滑块2的碰撞端面粘上橡皮泥(或双面胶纸)。
(4)用天平测出滑块1和滑块2的质量m1、m2。
(5)把滑块1和滑块2放在气垫导轨上,让滑块2处于静止状态( =0),用滑块1以初速度
=0),用滑块1以初速度 与之碰撞(这时光电计时器系统自动计算时间),撞后两者粘在一起,分别记下滑块1的挡光片碰前通过光电门的遮光时间
与之碰撞(这时光电计时器系统自动计算时间),撞后两者粘在一起,分别记下滑块1的挡光片碰前通过光电门的遮光时间 和碰后通过光电门的遮光时间
和碰后通过光电门的遮光时间 。
。
(6)先根据 计算滑块1碰撞前的速度
计算滑块1碰撞前的速度 及碰后两者的共同速度
及碰后两者的共同速度 ;再计算两滑块碰撞前后的动量,并比较两滑块碰撞前后的动量的矢量和。
;再计算两滑块碰撞前后的动量,并比较两滑块碰撞前后的动量的矢量和。
实验数据:
m1=0.324kg m2="0.181kg " L=1.00×10-3m
| 次 数 |
滑块1 |
滑块2 |
碰前系统动量kgms-1 |
碰后系统动量kgms-1 |
|||
 /ms-1 /ms-1 |
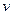 /ms-1 /ms-1 |
 /ms-1 /ms-1 |
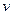 /ms-1 /ms-1 |
 |
 |
( + + ) )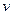 |
|
| 1 |
0.290 |
0.184 |
0 |
0.184 |
|
|
|
| 2 |
0.426 |
0.269 |
0 |
0.269 |
|
|
|
| 结论: |
|||||||
质量均为m的物体A和B分别系在一根不计质量的细绳两端,绳子跨过固定在倾角为30°的斜面顶端的定滑轮上,斜面固定在水平地面上,开始时把物体B拉到斜面底端,这时物体A离地面的高度为0.8米,如图所示.。若摩擦力均不计,从静止开始放手让它们运动.(斜面足够长,g取10m/s2)求: 
(1)物体A着地时的速度;
(2)物体A着地后物体B沿斜面上滑的最大距离.
如图所示,水平地面上固定着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径的10倍,且圆弧半径为R,整个轨道处于同一竖直平面内,可视为质点的物块从A点正上方某处无初速下落,恰好落入小车圆弧轨道上滑动,然后沿水平轨道滑行到轨道末端C,速度恰好为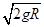 。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,不考虑空气阻力、墙壁的摩擦阻力和物块落入圆弧轨道时的能量损失.求:
。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,不考虑空气阻力、墙壁的摩擦阻力和物块落入圆弧轨道时的能量损失.求:
(1)物块开始下落的位置距水平轨道BC的竖直高度
(2)物块与水平轨道BC间的动摩擦因数μ
人类发射的空间探测器进入某行星的引力范围后,绕该行星做匀速圆周运动,已知该行星的半径为R,探测器运行轨道在其表面上空高为h处,运行周期为T,引力常量G,求:
(1)该行星的质量
(2)若探测器靠近行星表面飞行时,测得运行周期为T1,则行星平均密度为多少?(用T1和常数表达)
从某一高度平抛一物体,当抛出2S后它的速度方向与水平方向成45°,落地时速度方向与水平面成60°,g取10m/s2,求:
(1)抛出时的速度 (2)抛出点距地面的高度
如图所示,质量m=70kg的运动员以10m/s的速度,从高h=10m的滑雪场A点沿斜坡自由滑下,一切阻力可忽略不计。求: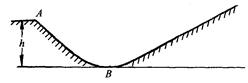
(1)运动员在A点时的机械能。
(2)运动员到达最低点B时的速度。
(3)若运动员继续沿斜坡向上运动,他能到达的最大高度。(g=10m/s2)