某数学家观察到：
；
；
；
，于是该数学家猜想：任何形如
都是质数，请判断该数学家的推理方式并对该结论给出正误判断（ ）．
| A．类比推理推理结果正确 | B．类比推理推理结果错误 |
| C．归纳推理推理结果正确 | D．归纳推理推理结果错误 |
用数学归纳法证明：1+2+22+…2n﹣1=2n﹣1（n∈N）的过程中，第二步假设当n=k时等式成立，则当n=k+1时应得到（）
| A．1+2+22+…+2k﹣2+2k+1﹣1 |
| B．1+2+22+…+2k+2k+1=2k﹣1+2k+1 |
| C．1+2+22+…+2k﹣1+2k+1=2k+1﹣1 |
| D．1+2+22+…+2k﹣1+2k=2k﹣1+2k |
证明1+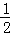
+…+
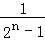
（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（）
| A．1项 | B．k﹣1项 | C．k项 | D．2k项 |
利用数学归纳法证明“（n+1）（n+2）…（n+n）=2n×1×3×…×（2n﹣1），n∈N*”时，从“n=k”变到“n=k+1”时，左边应增乘的因式是（）
| A．2k+1 | B． |
C． |
D． |
用数学归纳法证明不等式“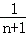
+
+…+
＞
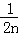（n＞2）”时的过程中，由n=k到n=k+1时，不等式的左边（）
A．增加了一项 |
B．增加了两项 |
C．增加了两项，又减少了一项 |
D．增加了一项，又减少了一项 |
某个命题与自然数n有关，若n=k（k∈N*）时命题成立，那么可推得当n=k+1时该命题也成立．现已知当n=5时，该命题不成立，那么可推得（）
| A．当n=6时，该命题不成立 | B．当n=6时，该命题成立 |
| C．当n=4时，该命题不成立 | D．当n=4时，该命题成立 |