求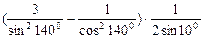 。
。
如图,已知等边△ABC,AB=16,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
(1)求证:DF是⊙O的切线;
(2)求FG的长;
(3)求tan∠FGD的值.
2014年1月10日,国内成品油价格迎来了首次降低,某调查员就“汽油降价对用车的影响”,
这一问题向有机动车的私家车车主进行了问卷调查,并制作了统计图表的一部分如下:
| 车主的态度 |
百分比 |
| A. 没有影响 |
4% |
| B. 影响不大 |
p |
| C. 有影响 |
52% |
| D. 影响很大 |
m |
| E. 不关心这个问题 |
10% |

(1)结合上述统计图表可得:p= ,m= ;
(2)根据以上信息,补全条形统计图;
(3)2014年1月末,某市有机动车的私家车车主约200 000人,根据上述信息,请你估计一下持有“影响不大”这种态度的车主约有多少人?
如图,在□ABCD中,E为BC边上的一点,将△ABE沿AE翻折得到△AFE,点F恰好落在线段DE上.
(1)求证:∠FAD=∠CDE;
(2)当AB=5,AD=6,且 时,求线段EC的长.
时,求线段EC的长.
列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出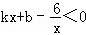 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.