
用均匀导线弯成正方形闭合金属线框abcd,线框每边长80cm,每边的电阻为0.01Ω。把线框放在磁感强度B=0.05T的匀强磁场中,并使它绕轴OO′以ω=100rad/s的角速度匀角速度旋转,旋转方向如图
(1)每条边产生的感应动势大小;
(2)线框内感应电流的大小;
(3)e,f分别是ab和cd的中点,ef两点间的电势差。
如图11-16所示,直角三角形导线框ABC,处于磁感强度为B的匀强磁场中,线框在纸面上绕B点以匀角速度ω作顺时针方向转动,∠B =60°,∠C=90°,AB=l,求A,C两端的电势差UAC。

共有100匝的矩形线圈,在磁感强度为0.1T的匀强磁场中以角速度ω=10rad/s绕线圈的中心轴旋转。已知线圈的长边a=20cm,短边b=10cm,线圈总电阻为2Ω。求(2)线圈平面转到与磁场方向夹角60°时,线圈受到的电磁力矩。
如图11-9所示,一个U形导体框架,其宽度L=1m,框架所在平面与水平面的夹用α=30°。其电阻可忽略不计。设匀强磁场与U形框架的平面垂直。匀强磁场的磁感强度B=0.2T。今有一条形导体ab,其质量为m=0.5kg,有效电阻R=0.1Ω,跨接在U形框架上,并且能无摩擦地滑动,求:
(1)由静止释放导体,导体ab下滑的最大速度vm;
(2)在最大速度vm时,在ab上释放的电功率。(g=10m/s2)。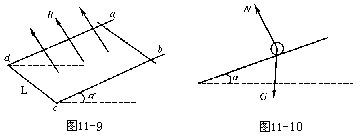
如图11-7所示装置,导体棒AB,CD在相等的外力作用下,沿着光滑的轨道各朝相反方向以0.lm/s的速度匀速运动。匀强磁场垂直纸面向里,磁感强度B=4T,导体棒有效长度都是L=0.5m,电阻R=0.5Ω,导轨上接有一只R′=1Ω的电阻和平行板电容器,它的两板间距相距1cm,试求:(l)电容器及板间的电场强度的大小和方向;