如图所示，质量为1.0g的带电小球，用长为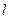
的绳线悬挂在平行板电容器之间，两板电压为40V，板间距10cm，小球在A点处于平衡状态悬线和竖直方向夹角为37°.问：
（1）小球电量多少?是正电还是负电?
（2）若把小球拉到θ＝53°的点，CB保持水平时受到的拉力为多大?
（3）若把BC剪断，小球摆到最低点O时，悬线的拉力多大?12分
一列简谐横波，在时刻
＝0时波形如图，波的传播方向向右，已知在
＝0.9s时刻A点出现第三次波峰，求：
(1)该波的周期多大？
(2)该波传播到B点需要多长时间？
(3)经过多长时间B点第一次出现波谷？
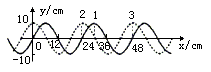
如下图所示图中的实线是一列简谐波在某一时刻的波形曲线．经0.2s后，其波形如图中虚线所示，设该波的周期T大于0.2s，求：
(1)从图中读出波的振幅和波长；
(2)如果波向右传播，波速是多大？波的周期是多大？
(3)如果波向左传播，波速是多大？波的周期是多大？
如图为某时刻t的横波图像，求：
(1)这列波的波长
和振幅A；
(2)若波沿x轴正方向传播，当波速为4m/s时，经1s时，A点位移是多大？B点通过的路程是多少？
(3)画出(t＋0.5)s时的波形图；
(4)画出x=6m处的质点从此刻(t时刻)起的振动图像．
在一列横波的传播方向上有相距1.2m的A．B两点．当波传到A点，且从A质点第一次到达正的最大位移处开始计时，测得4s时间里A质点恰好第9次到达正的最大位移处，而B质点在这4s时间内共6次到达正的最大位移处．这列波的传播速度在什么范围？
如图所示，是用干涉法检查某块厚玻璃板的上表面是否平滑的装置，a是一块标准样板，b是待检验的厚玻璃，c是很薄的垫块，将标准样板与待检验的玻璃之间形成一个很薄的楔形空气薄膜，所用的单色光是用普通光加滤光片产生的．试说明利用此法的原理．