一机车拉一拖车,由静止开始,在水平轨道上匀加速前进,经一段时间,通过路程 ,这时机车将拖车解脱,且保持牵引力不变,又经过同样的时间,机车和拖车相距为L,试求机车和拖车的质量之比M/m.(阻力不计)
,这时机车将拖车解脱,且保持牵引力不变,又经过同样的时间,机车和拖车相距为L,试求机车和拖车的质量之比M/m.(阻力不计)
用油膜法可粗略测出阿伏加德罗常数,把密度ρ=0.8×103 kg/m3的某种油,用滴管滴出一滴油在水面上形成的油膜,已知这滴油的体积V=0.5×10-3cm3,形成的油膜面积S="0.7" m2,油的摩尔质量Ml="0.09" kg/mol.若把油膜看成单分子层,每个油分子看成球形,那么:
(1)油分子的直径为多少?
(2)由以上数据可算出的阿伏加德罗常数大约为多少(保留一位有效数字)?
在做“用油膜法估测分子的大小”实验中,油酸酒精溶液的浓度为每104 mL溶液中有纯油酸6 mL.用注射器测得1 mL上述溶液中有液滴50滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,随后把玻璃板放在坐标纸上,其形状如图11-2所示,坐标中正方体小方格的边长为20 mm.求:
图11-2
(1)油酸膜的面积是多少?
(2)每一滴油酸酒精溶液中含有纯油酸的体积是多少?
(3)根据上述数据,估测出油酸分子的直径是多少?
下面关于布朗运动的两种说法都是错误的,试分析它们各错在哪里.
(1)在北方冬天的大风天气,经常看到风沙弥漫、尘土飞扬,这就是布朗运动;
(2)一滴碳素墨水滴在清水中,过一会儿整杯水都黑了,这是碳分子做无规则运动的结果.
“在测定某金属块的比热容时,先把质量已知的金属块放在沸水中加热.经过一段时间后把它迅速放进质量、温度均已知的水中,并用温度计测量水的温度.当水温不再上升时,这就是金属块与水的共同温度.根据实验数据就可以计算出金属块的比热容.”
以上叙述中,哪些地方涉及到了“平衡态”和“热平衡”的概念.
对于某体积不变的理想气体,温度每升高1℃,压强就增大了t0℃时物体压强的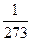 ,设t0℃时物体压强为p0,则温度为t时,物体压强为多少?(用两种方式表示)
,设t0℃时物体压强为p0,则温度为t时,物体压强为多少?(用两种方式表示)