如图电路中,电源电动势E=6V,内阻r=2Ω,电阻R1=1Ω,变阻器最大阻值R=10Ω.当滑片P由变阻器a端滑到b端的过程中,
(1)变阻器R多少Ω时,电阻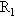 消耗的电功率最大,最大电功率
消耗的电功率最大,最大电功率 多少W.
多少W.
(2)变阻器R多少Ω时,电源输出的电功率最大,最大输出功率 多少W,此时电源释放的电功率
多少W,此时电源释放的电功率 多少W,电源供电效率η多少.
多少W,电源供电效率η多少.
(3)变阻器R多少Ω时,电源输出的电功率为4W.
根据量子理论,光子的能量满足关系式E=pc,其中c为光在真空中的速度,p为光子具有的动量.
有人设想利用光子被物体反射时对物体产生的压力作为宇宙探测器加速的动力.探测器上安装有面积很大,反射率极高的薄膜,使薄膜正对太阳. 已知太阳光照射到薄膜时每平方米面积上的功率为P0,探测器和薄膜的总质量为m,薄膜面积为S,每个光子的动量为p,不考虑万有引力等其它力的作用,试求
(1)经过时间t,照射到探测器薄膜表面的光子数;
(2)探测器的加速度有多大.
如图所示,轻绳绕过轻滑轮连接着边长为L的正方形导线框A1和物块A2,线框A1的电阻为R,质量为M,物块A2的质量为m(M>m),两匀强磁场区域I、II的高度也为L,磁感应强度均为B,方向水平与线框平面垂直。线框ab边距磁场边界高度为h。开始时各段绳都处于伸直状态,把它们由静止释放,ab边刚穿过两磁场的分界线CC进入磁场II时线框做匀速运动。求:
|
如图所示,空间存在垂直纸面向里的两个匀强磁场区域,磁感应强度大小均为B,磁场I宽为L,两磁场间的无场区域为II,宽也为L,磁场III宽度足够大。区域中两条平行光滑金属导轨间距为l,不计导轨电阻,两导体棒ab、cd的质量均为m,电阻均为r。ab棒静止在磁场I中的左边界处,cd棒静止在磁场III中的左边界处,对ab棒施加一个瞬时冲量,ab棒以速度 开始向右运动。
开始向右运动。
|
 ,求ab棒通过区域II的时间;
,求ab棒通过区域II的时间;
如图所示,两根不计电阻的倾斜平行导轨与水平面的夹角θ=37o ,底端接电阻R=1.5Ω。金属棒a b的质量为m=0.2kg。电阻r=0.5Ω,垂直搁在导轨上由静止开始下滑,金属棒a b与导轨间的动摩擦因数为μ=0.25,虚线为一曲线方程y=0.8sin( x)m与x轴所围空间区域存在着匀强磁场,磁感应强度.B=0.5T,方向垂直于导轨平面向上(取g=10m/s2,sin37o=0.6,cos37o=0.8)。求:
x)m与x轴所围空间区域存在着匀强磁场,磁感应强度.B=0.5T,方向垂直于导轨平面向上(取g=10m/s2,sin37o=0.6,cos37o=0.8)。求:
(1)当金属棒a b下滑的速度为 m/s 时,电阻R上消耗的电功率是多少?
m/s 时,电阻R上消耗的电功率是多少?
(2)若金属棒a b从静止开始运动到Xo="6" m处,电路中消耗的电功率为0.8w,在这一过程中,安培力对金属棒a b做了多少功?
2005年10月12日上午9时,“神舟六号”在长征2号F运载火箭的推动下飞向太空,飞船先在距近地点200km、远地点350km的椭圆型轨道上运行5圈后变轨进入到距地面343km的圆形轨道上绕地球飞行。与10月17日凌晨,返回舱顺利着陆。
为使问题简化,现设地球的半径为R,地球表面的重力加速度为g,地球自转周期为T,飞船做圆轨道飞行时距地面高度为H,求:飞船进入圆轨道做匀速圆周运动时的周期为多少?其轨道半径与地球同步卫星轨道半径之比为多少?(用以上字母表示)