据报道，最近已研制出一种可以投入使用的电磁轨道炮，其原理如图所示．炮弹(可视为长方形导体)置于固定在水平面上的两平行导轨之间，并与轨道壁密接．开始时，炮弹静止在轨道的一端，通以电流后炮弹会在磁场力的作用下被加速，最后从位于导轨另一端的出口高速射出．假设两导轨间的距离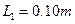
，导轨长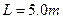
，炮弹的质量m="0.30" kg，导轨上的电流I的方向如图中箭头所示．炮弹在轨道内运动时可认为它所在处磁场的磁感应强度始终为B=2.0T，方向垂直于纸面向里，忽略炮弹与导轨间的摩擦．若炮弹的出口速度
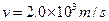，求通过导轨的电流I．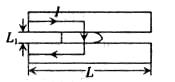
用如图所示的装置可以测量汽车在水平路面上做匀加速直线运动的加速度。该装置是在矩形箱子的前、后壁上各安装一个由力敏电阻组成的压力传感器。用两根相同的轻弹簧夹着一个质量为2.0kg的滑块，滑块可无摩擦的滑动，两弹簧的另一端分别压在传感器a、b上，其压力大小可直接从传感器的液晶显示屏上读出。现将装置沿运动方向固定在汽车上，传感器b在前，传感器a在后，汽车静止时，传感器a、b的示数均为10N（取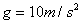
）
（1）若传感器a的示数为14N、b的示数为6.0N，求此时汽车的加速度大小和方向。
（2）当汽车以怎样的加速度运动时，传感器a的示数为零。
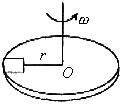
如图所示，水平转盘上放有质量为m的物块，当物块到转轴的距离为r时，连接物块和转轴的绳刚好被拉直（绳上张力为零）。物体和转盘间最大静摩擦力是其正压力的μ倍，求：
（1）当转盘的角速度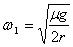
时，细绳的拉力
。
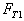（2）当转盘的角速度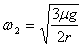
时，细绳的拉力
。
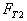质量为m的小球A沿光滑水平面以速度v0与质量为2m静止的小球B发生正碰，碰撞后，A球的动能变为原来的1/9，那么小球B的速度是多少？
如图所示，A、B两棒均长l m，A悬于高处，B竖于地面．A的下端和B的上端相距s="10" m．若A、B两棒同时运动，A做自由落体运动，B以初速度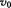
= 20m／s做竖直上抛运动，在运动过程中都保持竖直．问：
(1)两棒何时开始相遇?
(2)擦肩而过(不相碰)的时间?(取g="10" m／s2)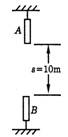
甲车以10米/秒，乙车以4米/秒的速率在同一直车道中同向前进，若甲车驾驶员在乙车后方距离d处发现乙车，立即踩刹车使其车获得－2米/秒2的加速度，为使两车不致相撞，d的值至少应为多少？