已知平面内两定点
，动点
满足条件：
，设点的轨迹是曲线
为坐标原点。
（I）求曲线
的方程；
（II）若直线
与曲线相交于两不同点
，求
的取值范围；
（III）（文科做）设
两点分别在直线
上，若
，记
分别为两点的横坐标，求
的最小值。
（理科做）设两点分别在直线上，若，求
面积的最大值。
如图，椭圆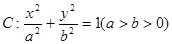
经过点
，离心率
，直线l的方程为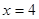
．
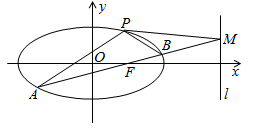
（1）求椭圆C的方程；
（2）
是经过右焦点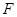
的任一弦（不经过点
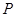），设直线与直线
相交于点
，记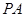
、
、
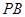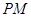的斜率分别为
、
、
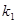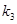．问：是否存在常数
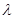，使得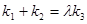
? 若存在，求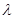的值； 若不存在，请说明理由．
经销商经销某种农产品，在一个销售季度内，每售出1t该产品可获得利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该产品，以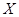
（单位：t，
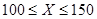）表示下一个销售季度内的市场需求量，
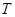（单位：元）表示下一个销售季度内该农产品的销售利润．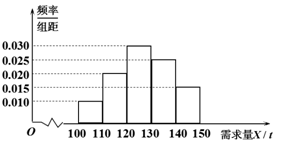
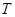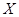（1）将表示为的函数；
（2）根据直方图估计利润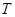不少于57000元的概率．
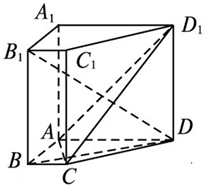
如图，在直棱柱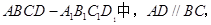
（1）证明：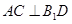
；
（2）求直线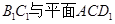
所成角的正弦值．
设关于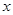
的一元二次方程
．
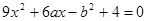（1）若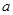
是从1，2，3这三个数中任取的一个数，
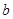是从0，1，2这三个数中任取的一个数，求上述方程有实根的概率；
（2）若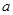是从区间[0，3]中任取的一个数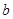，是从区间[0，2]中任取的一个数，求上述方程有实根的概率．
已知命题
命题
若命题“
”是真命题，求实数
的取值范围．