一客车从静止开始以加速度a做匀加速直线运动的同时,在车尾的后面离车头为s m远的地方有一乘客以某一速度正在追赶这列客车.已知司机从车头前面的反光镜内能看到离车头的最远距离为s0 m,保留时间在t0 s内才能看清楚,这样才能制动客车使车停下来,该乘客要想乘坐上这列客车,追赶客车匀速运动的速度所满足条件的表达式是什么?若a="1.0" m/s2,s="30" m,s0="20" m,t0="1.0" s,求v的最小值.
如图11-9所示,竖直平面内有足够长的金属导轨,轨距0.2m,金属导体ab可在导轨上无摩擦地上下滑动,ab的电阻为0.4Ω,导轨电阻不计,导轨ab的质量为0.2g,垂直纸面向里的匀强磁场的磁应强度为0.2T,且磁场区域足够大,当ab导体自由下落0.4s时,突然接通电键K,则:(1)试说出K接通后,ab导体的运动情况。(2)ab导体匀速下落的速度是多少?(g取10m/s2)
如图11-7所示装置,导体棒AB,CD在相等的外力作用下,沿着光滑的轨道各朝相反方向以0.lm/s的速度匀速运动。匀强磁场垂直纸面向里,磁感强度B=4T,导体棒有效长度都是L=0.5m,电阻R=0.5Ω,导轨上接有一只R′=1Ω的电阻和平行板电容器,它的两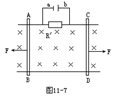 板间距相距1cm,试求:
板间距相距1cm,试求:
(l)电容器及板间的电场强度的大小和方向;
如图11-6所示,在跟匀强磁场垂直的平面内放置一个折成锐角的裸导线MON,∠MON=α。在它上面搁置另一根与ON垂直的导线PQ,PQ紧贴MO,ON并以平行于ON的速度V,从顶角O开始向右匀速滑动,设裸导线单位长度的电阻为R0,磁感强度为B,求回路中的感应电流。
如图11-3所示,直角三角形导线框ABC,处于磁感强度为B的匀强磁场中,线框在纸面上绕B点以匀角速度ω作顺时针方向转动,∠B=60°,∠C=90°,AB=l,求A,C两端的电势UAC。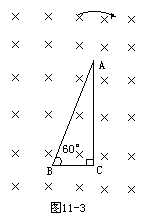
如图11-2所示,以边长为50cm的正方形导线框,放置在B=0.40T的身强磁场中。已知磁场方向与水平方向成37°角,线框电阻为0.10Ω,求线框绕其一边从水平方向转至竖直方向的过程中通过导线横截面积的电量。