一级方程式汽车大赛中,一辆赛车总质量为m,一个路段的水平转弯半径为R,赛车转此弯时的速度为v,赛车形状都设计得使其上下方空气有一压力差——气动压力,从而增大了对地面的正压力.正压力与摩擦力的比值叫侧向附着系数,以η表示.要上述赛车转弯时不侧滑,则需要多大的气动压力?
电饭锅是一种可以自动煮饭并自动保温,又不会把饭烧焦的家用电器。它的电路由控制部分AB和工作部分BC组成。K1是限温开关,手动闭合,当温度达到1030C时自动断开,不能自动闭合。K2是自动开关,当温度超过800C时自动断开,温度低于700C时自动闭合。R2是限流电阻,阻值2140Ω,R1是工作电阻,阻值60Ω。锅中放好适量的米和水,插上电源(220V,50HZ),手动闭合K1后,电饭锅就能自动煮好米饭并保温。
⑴简述手动闭合K1后,电饭锅加热、保温过程的工作原理。
⑵加热过程电饭锅消耗的电功率P1是多大?K1、K2都断开时电饭锅消耗的功率P2是多大?
⑶若插上电源后没有手动闭合K1,能煮熟饭吗?为什么?
如图所示, 微法,
微法, 微法,
微法, 欧,
欧, 欧,当开关S断开时,A、B两点电压
欧,当开关S断开时,A、B两点电压 当S闭合时,C1的电量是增加还是减少?改变了多少库仑?已知
当S闭合时,C1的电量是增加还是减少?改变了多少库仑?已知 伏。
伏。
如图所示的电路中,电池的电动势ε=5伏,内电阻r=10欧,固定电阻R=90欧,R0是可变电阻,在R0由零增加到400欧的过程中,求:
(1)可变电阻R0消耗功率最大的条件和最大热功率。
(2)电池的内电阻r和固定电阻R上消耗的最小热功率之和。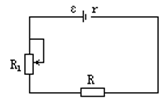
如图所示电路中,当滑动变阻器的滑片P向左移动时,各表(各电表内阻对电路的影响均不考虑)的示数如何变化?为什么?
用伏安法测一节干电池的电动势和内电阻,伏安图象如图所示,根据图线回答:
(1)干电池的电动势和内电阻各多大?
(2)图中a点对应的外电路电阻是多大?电源此时内部热功率是多少?
(3)图中a、b两点对应的外电路电阻之比是多大?对应的输出功率之比是多大?
(4)在此实验中,电源最大输出功率是多大?