如图1所示，a、b和c为质量相等的三个弹性小球（可视为质点），a、b分别悬挂在l1=1m、l2=0.25m的轻质细线上，它们刚好与光滑水平面接触而不互相挤压，a、b相距10cm。若c从a和b的连线中点处以v0=5cm/s的速度向右运动，则c将与a和b反复碰撞而往复运动。已知碰撞前后小球c均沿同一直线运动，碰撞时间极短，且碰撞过程中没有机械能损失，碰撞后a和b的摆动均可视为简谐运动。以c球开始运动作为时间零点，以向右为正方向，试简述小球c的运动情况并在图2中画出在10s内c球运动的位移一时间图象，图象以c球的初位置为坐标原点。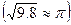
如图15-31所示，一等腰直角棱镜，放在真空中，AB=AC=d.在棱镜侧面AB左方有一单色点光源S，从S发出的光线SD以60°的入射角从AB侧面中点射入，当它从AC侧面射出时，出射光线偏离入射光线的偏向角为30°，若测得光从光源到棱镜侧面AB的时间跟在棱镜中传播时间相等，那么点光源S到棱镜AB侧面的垂直距离是多少？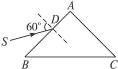
图15-31
半径为R的玻璃半圆柱体，横截面如图13-4-8所示，圆心为O，两条平行单色红光沿截面射向圆柱面，方向与底面垂直，光线1的入射点A为圆柱面的顶点，光线2的入射点为B，∠AOB=60°，已知该玻璃对红光的折射率n=
.
图13-4-8
（1）求两条光线经柱面和底面折射后的交点与O点的距离d；
（2）若入射的是单色蓝光，则距离d将比上面求得的结果大还是小?
为了减少光在透镜表面由于反射带来的损失,可在透镜表面涂上一层增透膜.已知增透膜的折射率为1.4,绿光的波长为5 600
.为了使其在垂直表面入射的使反射光干涉消失,求所涂的这种增透膜的最小厚度.
如图19-4-15所示，宽为a的平行光束从空气斜射到两面平行的玻璃板上表面，入射角为45°.光束中包含两种波长的光，玻璃对这两种波长光的折射率分别为n1=1.5,n2=
.
图19-4-15
（1）求每种波长的光射入上表面后的折射角r1、r2.
（2）为使光束玻璃下表面出射时能分成不交叠的两束，玻璃板的厚度d至少为多少？并画出光路示意图.
如图19-4-12所示，等腰直角棱镜ABO的两腰长都是16 cm.为了测定它的折射率，棱镜放在直角坐标系中，使两腰与Ox、Oy轴重合.从OB边的C点注视A棱，发现A棱的视位置在OA边上的D点，在C、D两点插上大头针，看出C点的坐标为（0，12），D点的坐标为（9，0）.由此计算出该棱镜的折射率为多少？