如图所示,带正电的小球套在绝缘的长直杆上,球与杆之间的动摩擦因素为μ,匀强电场水平向右,将杆与竖直线分别成不同角度固定放置,让小球由静止释放后都沿杆运动距离s,当杆与竖直线的夹角为θ时,小球获得的末动能最大为E.现将杆竖直固定放置,为使小球由静止释放后获得的动能与前面的动能E相等,小球运动的距离 应是多少?
应是多少?
如图13-21所示,横截面是直角三角形ABC的三棱镜对红光的折射率为n1,对紫光的折射率为n2。一束很细的白光由棱镜的一个侧面AB垂直射入,从另一侧面AC折射出来。已知棱镜顶角∠A=30°,AC边平行于光屏MN,且与光屏的距离为L。
图13-21
(1)画出白光通过棱镜的光路图(出射光线只画出两条边缘光线,并指明其颜色)。
(2)求在光屏MN上得到的彩色光带的宽度d。
一辆实验小车可沿水平地面(图中纸面)上的长直轨道匀速向右运动.有一台发出细光束的激光器装在小转台M上,到轨道的距离MN为d="10" m,如图14-10所示,转台匀速转动,使激光束在水平面内扫描,扫描一周的时间为T="60" s,光束转动方向如图中箭头所示,当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过Δt="2.5" s光束又射到小车上,则小车的速度为多少?(结果保留两位有效数字)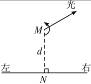
图14-10
如图14-7所示,置于空气中的一个不透明容器内盛满某种透明液体.容器底部靠近器壁处有一竖直放置的6.0 cm长的线光源.靠近线光源一侧的液面上盖有一遮光板,另一侧有一水平放置的与液面等高的望远镜,用来观察线光源.开始时通过望远镜不能看到线光源的任何一部分.将线光源沿容器底向望远镜一侧平移至某处时,通过望远镜刚好可以看到线光源底端,再将线光源沿同一方向移动8.0 cm,刚好可以看到其顶端.求此液体的折射率n.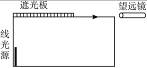
图14-7
如图14-2-10所示,相距为d的两平行金属板A、B足够大,板间电压恒为U,有一波长为λ的细激光束照射到B板中央,使B板发生光电效应,已知普朗克常量为h,金属板B的逸出功为W,电子质量为m,电荷量e,求: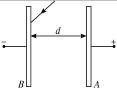
图14-2-10
(1)从B板运动到A板所需时间最短的光电子到达A板时的动能;
(2)光电子从B板运动到A板时所需的最长时间.
德布罗意认为,任何一个运动着的物体,都有一种波与它对应,波长是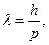 式中p是运动物体的动量,h是普朗克常量.已知某种紫光的波长是440 nm,若将电子加速,使它的德布罗意波长是这种紫光波长的10-4倍,求:
式中p是运动物体的动量,h是普朗克常量.已知某种紫光的波长是440 nm,若将电子加速,使它的德布罗意波长是这种紫光波长的10-4倍,求:
(1)电子的动量的大小.
(2)试推导加速电压跟德布罗意波长的关系,并计算加速电压的大小.电子质量m=9.1×10-31 kg,电子电荷量e=1.6×10-19 C,普朗克常量h=6.6×10-34 J·s,加速电压的计算结果取一位有效数字.