如图13-7-14所示,在匀强电场中,电荷量q=5.0×10-10 C的正电荷,由a点移到b点和由a点移到c点,电场力做功都是3.0×10-8 J.已知a、b、c三点的连线组成直角三角形,ab="20" cm,∠a=37°,∠c=90°,求: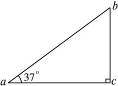
图13-7-14
(1)a、b两点的电势差Uab;
(2)匀强电场的场强大小和方向.
已知在一个LC回路中,电容C="0.04" μF,电感L=6.4mH,求这个回路的固有频率是多少.
有一理想的LC振荡电路,电容器的电容为C,线圈的自感系数为L,开始时电容器两端电压为U,电路中无电流,先让C通过L放电,到放电结束为止,在放电过程中的平均电流为多大?
一个LC振荡电路,可变电容器的最大电容Cmax="400" pF,要求产生的振荡电流的频率范围是535 kHz~1 605 kHz,求:
(1)线圈的自感系数;
(2)可变电容器的电容变化范围.
振荡电路中的电容为30—390 pF可变,电感为88.6×10-3 H,振荡电路中产生的振荡电流的周期在什么范围内?如果电容器的电容为C1时,电路中的最大电流为I1,保持电容器的最大带电荷量不变,突然将C1减小到C2,电路中的最大电流为I2,试比较I1与I2.
一个LC振荡电路,线圈的自感系数可从L1="0.1" mH变到L2="4" mH,电容器的电容可以从C1="36" pF变到C2="90" pF,求该振荡电路的最大振荡周期和最大振荡频率.