(sin = 0.6,cos
= 0.6,cos = 0.8,tan
= 0.8,tan = 0.75,cot
= 0.75,cot = 1.33)
= 1.33)
一台电动机,它的额定电压是220V,电阻是0.5Ω,在正常工作时,通过这台电动机的电流强度是50A,当电动机正常工作时,试求:
⑴2s内电动机消耗的电能是多少?
⑵2s内电动机产生的电热是多大?
⑶2s内电动机输出的机械能是多大?
在磁感应强度为2.0T的匀强磁场中,放一条与磁场方向垂直的长度为0.5m的通电导线,导线中的电流为4.0A.这段导线在与磁场方向垂直的光滑绝缘水平面内,沿安培力的方向从静止开始移动了3.0m.试求:
⑴导线在磁场中受到的安培力大小;
⑵安培力对导线所做的功;
⑶导线获得的动能.
真空中有两个完全相同的带电小球,相距0.3m,它们的电荷量分别是+2.0×10 - 9C和-4.0×10 - 9C,问:
⑴这两个电荷的相互作用力是引力还是斥力?
⑵这两个电荷的相互作用力为多大?
⑶当两电荷接触后再放回原处,这两个电荷的相互作用力又如何?
如图所示,一质量为m,带电荷量为+q的粒子以速度 从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从点b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强为E、方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方的c点,如图所示.粒子的重力不计,试求:
从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从点b处穿过x轴,速度方向与x轴正方向的夹角为30°,同时进入场强为E、方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方的c点,如图所示.粒子的重力不计,试求:
⑴圆形匀强磁场的最小面积.
⑵粒子在磁场中运动的时间.
⑶c点到b点的距离d.
如图所示的电路中, =3.5Ω,
=3.5Ω,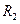 =6Ω,
=6Ω,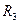 =3Ω,电压表为理想电表,当开关S断开时,电压表示数为5.7V;当开关S闭合时,电压表示数为3.5V.求电源的电动势和内电阻.
=3Ω,电压表为理想电表,当开关S断开时,电压表示数为5.7V;当开关S闭合时,电压表示数为3.5V.求电源的电动势和内电阻.