如图所示,长为0.48m的木板A,质量为1kg,板的右端放有物块B,质量为3kg,它们一起在光滑水平面上向左匀速运动,速度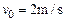 ,以后木板与等高的竖直固定档板C发生碰撞,碰撞时间极短,且碰撞时没有机械能损失,物块B与木板A间的动摩擦因数
,以后木板与等高的竖直固定档板C发生碰撞,碰撞时间极短,且碰撞时没有机械能损失,物块B与木板A间的动摩擦因数 ,取重力加速度
,取重力加速度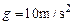 ,问A、C能否发生第二次碰撞,请通过计算说明理由.若能,则第一次碰撞后再经多长时间A与C发生第二次碰撞;若不能,则第一次碰撞后A做什么运动.
,问A、C能否发生第二次碰撞,请通过计算说明理由.若能,则第一次碰撞后再经多长时间A与C发生第二次碰撞;若不能,则第一次碰撞后A做什么运动.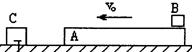
如图所示,质量为2kg的物块A(可看作质点),开始放在长木板B的左端,B的质量为1kg,可在水平面上无摩擦滑动,两端各有一竖直挡板MN,现A、B以相同的速度v0=6m/s向左运动并与挡板M发生碰撞.B与M碰后速度立即变为零,但不与M粘接;A与M碰撞没有能量损失,碰后接着返向N板运动,且在与N板碰撞之前,A、B均能达到共同速度并且立即被锁定,与N板碰撞后A、B一并原速反向,并且立刻解除锁定.A、B之间的动摩擦因数μ=0.1.通过计算回答下列问题:
(1)A与挡板M能否发生第二次碰撞?
(2)A和最终停在何处?
(3)A在B上一共通过了多少路程?
如图所示,右端有固定挡板的滑块B放在光滑的水平面上.B的质量为M=0.8kg,右端离墙壁的距离L=0.09m.在B 上靠近挡板处放一质量m=0.2kg的小金属块A,A与挡板之间有少量炸药.A和B之间的动摩擦因数μ=0.2.点燃炸药,瞬间释放出化学能.设有E0=0.5J的能量转化为A和B的动能.当B向右运动与墙壁发生碰撞后,立即以碰撞前的速率向左运动.A始终未滑离B.g=10m/s2.求: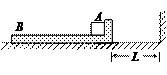
(1)A和B刚开始运动时的速度vA、vB;
(2)最终A在B上滑行的距离s.
如图所示,在光滑的水平面上固定有左、右两竖直挡板,挡板间距离足够长,有一质量为M,长为L的长木板靠在左侧挡板处,另有一质量为m的小物块(可视为质点),放置在长木板的左端,已知小物块与长木板间的动摩擦因数为μ,且M>m.现使小物块和长木板以共同速度v0向右运动,设长木板与左、右挡板的碰撞中无机械能损失.试求: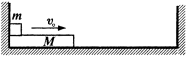
(1)将要发生第二次碰撞时,若小物块仍未从长木板上落下,则它应距长木板左端多远?
(2)为使小物块不从长木板上落下,板长L应满足什
么条件?
(3)若满足(2)中条件,且M=2kg,m=1kg,v0=10m/s,试计算整个系统在刚发生第四次碰撞前损失的机械能.
如图所示,质量为m=5kg的长木板放在水平地面上,在木板的最右端放一质量也为m=5kg的物块A.木板与地面间的动摩擦因数μ1=0.3,物块与木板间的动摩擦因数μ2=0.2.现用一水平力F=60N作用在木板上,使木板由静止开始匀加速运动,经过t=1s,撤去拉力.设物块与木板间的最大静摩擦力等于滑动摩擦力.(g取10m/s2)求: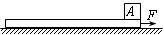
(1)拉力撤去时,木板的速度大小.
(2)要使物块不从木板上掉下,木板的长度至少多大.
(3)在满足(2)的条件下,物块最终将停在距板右端多远处.